题目内容
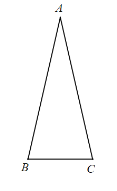
【题目】如图,![]()
![]() 中,
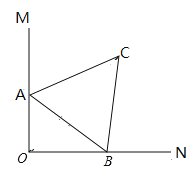
中,![]() 的顶点
的顶点![]() 分别在
分别在![]() 上,当点
上,当点![]() 在边
在边![]() 上运动时,点
上运动时,点![]() 随之在边
随之在边![]() 上运动,
上运动,![]() 的形状保持不变,在运动过程中,点
的形状保持不变,在运动过程中,点![]() 到点
到点![]() 的最大距离为( )
的最大距离为( )
A.7B.5C.4D.3
【答案】A
【解析】
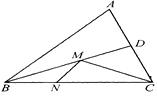
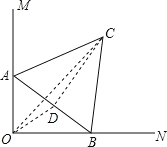
取AB的中点D,连接CD,根据三角形的边角关系得到OC≤OD+DC,只有当O、D及C共线时,OC取得最大值,最大值为OD+CD,根据D为AB中点,得到BD=3,根据三线合一得到CD垂直于AB,在Rt△BCD中,根据勾股定理求出CD的长,在Rt△AOB中,OD为斜边AB上的中线,根据直角三角形斜边上的中线等于斜边的一半可得OD的值,进而求出DC+OD,即为OC的最大值.
取AB的中点D,连接CD,
∵AC=BC=5,AB=6,
∵点D是AB边中点,
∴BD=![]() AB=3,CD⊥AB,
AB=3,CD⊥AB,
∴CD=![]() ,
,
连接OD,OC,有OC≤OD+DC,
当O、D.、C共线时,OC有最大值,最大值=OD+CD,
∵△AOB为直角三角形,D为斜边AB的中点,
∴OD=![]() AB=3,
AB=3,
∴OD+CD=3+4=7,即OC的最大值=7.
故选A.

练习册系列答案
相关题目