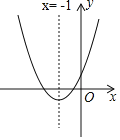题目内容
【题目】如图，二次函数y＝ax2+4x+c的图象与x轴交于A、B两点，与y轴交于点C，其中A（﹣1，0），C（0，5）
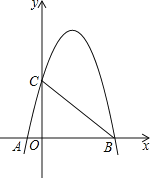
（1）求二次函数的解析式，并求出当x＝1时的函数值．
（2）连接BC，AC，得到△ABC，现将抛物线图象只向下平移m个单位，使得顶点落在△ABC内部（不包括边界），请写出m的取值范围．
【答案】（1）函数解析式为y＝﹣x2+4x+5；当x＝1时，y＝8；（2）6＜m＜9
【解析】
（1）利用待定系数法求抛物线解析式，然后把x＝1代入抛物线解析式可得到对应的函数值；
（2）先利用配方法得到抛物线的顶点坐标为（2，9），再解方程﹣x2+4x+5＝0得到B（5，0），则易得直线BC的解析式为y＝﹣x+5，由于x＝2对应的一次函数值为3，从而可确定m的范围．
解：（1）将（﹣1，0）和（0，5）代入y＝ax2+4x+c得
，解得
，
∴函数解析式为y＝﹣x2+4x+5；
当x＝1时，y＝﹣1+4+5＝8；
（2）∵y＝﹣x2+4x+5＝﹣（x﹣2）2+9
∴抛物线的顶点坐标为（2，9），
当y＝0时，﹣x2+4x+5＝0，解得x1＝﹣1，x2＝5，则B（5，0）
易得直线BC的解析式为y＝﹣x+5，
当x＝2时，y＝﹣x+5＝3，
∴抛物线图象只向下平移m个单位，使得顶点落在△ABC内部（不包括边界）时m的范围为6＜m＜9．
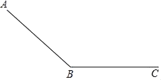
【题目】一个滑道由滑坡（AB段）和缓冲带（BC段）组成，如图所示，滑雪者在滑坡上滑行的距离y（单位：m）和滑行时间t1（单位：s）满足二次函数关系，并测得相关数据：
滑行时间t1/s | 0 | 1 | 2 | 3 | 4 |
滑行距离y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
滑雪者在缓冲带上滑行的距离y2（单位：m）和在缓冲带上滑行时间t2（单位：s）满足：y2＝52t2﹣2t22，滑雪者从A出发在缓冲带BC上停止，一共用了23s，则滑坡AB的长度（ ）米
A.270B.280C.375D.450
【题目】某商店销售一种商品，童威经市场调查发现：该商品的周销售量
（件）是售价
（元/件）的一次函数，其售价、周销售量、周销售利润
（元）的三组对应值如下表：
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注：周销售利润＝周销售量×（售价－进价）
（1）①求关于的函数解析式（不要求写出自变量的取值范围）
②该商品进价是_________元/件；当售价是________元/件时，周销售利润最大，最大利润是__________元
（2）由于某种原因，该商品进价提高了
元/件
，物价部门规定该商品售价不得超过65元/件，该商店在今后的销售中，周销售量与售价仍然满足（1）中的函数关系．若周销售最大利润是1400元，求的值
【题目】某公园划船项目收费标准如下：某班18名同学一起去该公园划船，若每人划船的时间均为1小时，则租船的总费用最低为_____元．
船型 | 两人船（限乘两 人） | 四人船（限乘四 人） | 六人船（限乘六 人） | 八人船（限乘八 人） |
每船租金（元/小时） | 50 | 80 | 100 | 120 |
