Question

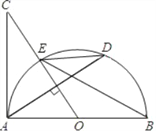
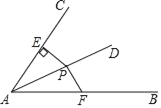
【题目】如图，点P是∠BAC的平分线AD上一点，PE⊥AC于点E，且AP＝2，∠BAC＝60°，有一点F在边AB上运动，当运动到某一位置时△FAP面积恰好是△EAP面积的2倍，则此时AF的长是______．

Answer 1

【答案】6．

【解析】

作PH⊥AB于H，根据角平分线的性质得到PH=PE，根据余弦的定义求出AE，根据三角形的面积公式计算即可．

作PH⊥AB于H，

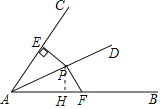
∵AD是∠BAC的平分线，PE⊥AC，PH⊥AB，

∴PH=PE，

∵P是∠BAC的平分线AD上一点，

∴∠EAP=30°，

∵PE⊥AC，

∴∠AEP=90°，

∴AE=AP×cos∠EAP=3，

∵△FAP面积恰好是△EAP面积的2倍，PH=PE，

∴AF=2AE=6，

故答案为：6．