Question

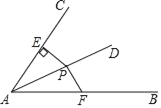
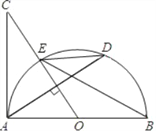
【题目】如图,AB是⊙O的直径,过圆心O作弦AD垂线交半⊙O于点E,交AC于点C,使∠BED=∠C．

（1）求证：AC是半⊙O的切线；

（2）若AC=8，cos∠BED=0.8，求线段AD的长．

Answer 1

【答案】（1）AC与圆O相切．证明见解析；（2）．

【解析】分析：（1）根据OC⊥AD，可得,然后根据∠C=∠BED=∠2，证明，据此即可证得AC与相切；
（2）在直角△AOC中利用三角函数和勾股定理求得OC和OA的长度，然后利用三角形的面积公式求得AF的长，再根据垂径定理求解．

详解：(1)AC与圆O相切.证明如下：

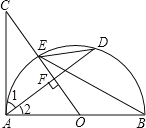
∵OC⊥AD，

∴,

∵∠C=∠BED=∠2，

∴,即

∴AC与相切；

(2)∵∠BED=∠C，

∴直角△AOC中,

∴

∴

又∵

∴

∵OC⊥AD，

∴