Question

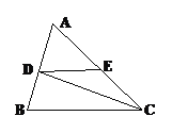
【题目】如图，CD是∠ACB的平分线，∠EDC=25，∠DCE=25，∠B=70．

（1）试证明：DE∥BC；

（2）求∠BDC的度数．

Answer 1

【答案】(1)答案见解析；（2）∠BDC=85°．

【解析】

（1）先利用角平分线的定义求出∠DCB的度数，等量代换得出∠DCB=∠EDC=25°，进而根据内错角相等两直线平行得出结论；
（2）利用两直线平行同旁内角互补求角的度数即可．

（1）∵CD平分∠ACB

∴∠ACD=∠BCD=25°

∵∠EDC=25°

∴∠EDC=∠BCD=25°

∴DE//BC.

（2）解：∵DE∥BC．
∵∠BDE+∠B=180°，
∴∠BDE=180°-70°=110°．
∵∠BDC+∠EDC=110°，
∴∠BDC=110°-∠EDC=85°．