Question

【题目】如图，六边形ABCDEF的内角都相等，CF∥AB．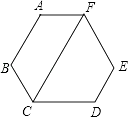
（1）求∠FCD的度数；
（2）求证：AF∥CD．

Answer 1

【答案】
（1）解：∵六边形ABCDEF的内角相等，

∴∠B=∠A=∠BCD=120°，

∵CF∥AB，

∴∠B+∠BCF=180°，

∴∠BCF=60°，

∴∠FCD=60°

（2）解：∵∠AFC=360°﹣120°﹣120°﹣60°=60°，

∴∠AFC=∠FCD，

∴AF∥CD．

【解析】（1）先求六边形ABCDEF的每个内角的度数，根据平行线的性质可求∠B+∠BCF=180°，再根据四边形的内角和是360°，求∠FCD的度数，从而求解．（2）先根据四边形内角和求出∠AFC=60°，再根据平行线的判定即可求解．
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识，掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质，以及对多边形内角与外角的理解，了解多边形的内角和定理：n边形的内角和等于（n-2）180°.多边形的外角和定理：任意多边形的外角和等于360°．