题目内容
【题目】问题探究
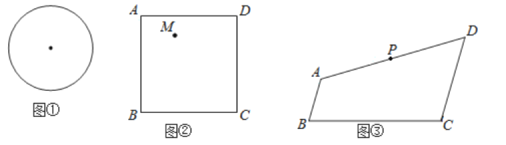
(1)请在图①中作出两条直线,使它们将圆面四等分;
(2)如图②,![]() 是正方形
是正方形![]() 内一定点,请在图②中作出两条直线(要求其中一条直线必须过点
内一定点,请在图②中作出两条直线(要求其中一条直线必须过点![]() ),使它们将正方形
),使它们将正方形![]() 的面积四等分:
的面积四等分:
问题解决
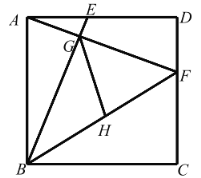
(3)如图③,在四边形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点如果
的中点如果![]() ,且
,且![]() ,那么在边
,那么在边![]() 上足否存在一点
上足否存在一点![]() ,使
,使![]() 所在直线将四边形
所在直线将四边形![]() 的面积分成相等的两部分?若存在,求出
的面积分成相等的两部分?若存在,求出![]() 的长:若不存在,说明理由.
的长:若不存在,说明理由.
【答案】(1)答案见解析;(2)答案见解析;(3)存在,BQ=b
【解析】
(1)画出互相垂直的两直径即可;
(2)连接AC、BD交于O,作直线OM,分别交AD于P,交BC于Q,过O作EF⊥OM交DC于F,交AB于E,则直线EF、OM将正方形的面积四等分,根据三角形的面积公式和正方形的性质求出即可;
(3)当BQ=CD=b时,PQ将四边形ABCD的面积二等份,连接BP并延长交CD的延长线于点E,证△ABP≌△DEP求出BP=EP,连接CP,求出S△BPC=S△EPC,作PF⊥CD,PG⊥BC,由BC=AB+CD=DE+CD=CE,求出S△BPC-S△CQP+S△ABP=S△CPE-S△DEP+S△CQP,即可得出S四边形ABQP=S四边形CDPQ即可.
解:(1)如图1所示,

(2)连接AC、BD交于O,作直线OM,分别交AD于P,交BC于Q,过O作EF⊥OM交DC于F,交AB于E,
则直线EF、OM将正方形的面积四等分,
理由是:∵点O是正方形ABCD的对称中心,
∴AP=CQ,EB=DF,
在△AOP和△EOB中
∵∠AOP=90°-∠AOE,∠BOE=90°-∠AOE,
∴∠AOP=∠BOE,
∵OA=OB,∠OAP=∠EBO=45°,
∴△AOP≌△EOB,
∴AP=BE=DF=CQ,
设O到正方形ABCD一边的距离是d,
则![]() (AP+AE)d=
(AP+AE)d=![]() (BE+BQ)d=
(BE+BQ)d=![]() (CQ+CF)d=
(CQ+CF)d=![]() (PD+DF)d,
(PD+DF)d,
∴S四边形AEOP=S四边形BEOQ=S四边形CQOF=S四边形DPOF,
直线EF、OM将正方形ABCD面积四等份;
(3)存在,当BQ=CD=b时,PQ将四边形ABCD的面积二等份,
理由是:如图③,连接BP并延长交CD的延长线于点E,
∵AB∥CD,
∴∠A=∠EDP,
∵在△ABP和△DEP中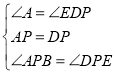
∴△ABP≌△DEP(ASA),
∴BP=EP,
连接CP,
∵△BPC的边BP和△EPC的边EP上的高相等,
又∵BP=EP,
∴S△BPC=S△EPC,
作PF⊥CD,PG⊥BC,则BC=AB+CD=DE+CD=CE,
由三角形面积公式得:PF=PG,
在CB上截取CQ=DE=AB=a,则S△CQP=S△DEP=S△ABP
∴S△BPC-S△CQP+S△ABP=S△CPE-S△DEP+S△CQP
即:S四边形ABQP=S四边形CDPQ,
∵BC=AB+CD=a+b,
∴BQ=b,
∴当BQ=b时,直线PQ将四边形ABCD的面积分成相等的两部分.