Question

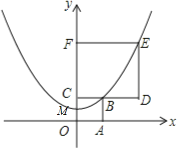
【题目】如图，正方形OABC和正方形CDEF在平面直角坐标系中，点O，C，F在y轴上，点O为坐标原点，点M为OC的中点，抛物线y=ax2+b经过M，B，E三点，则的值为 ．

Answer 1

【答案】1+．

【解析】

试题分析：设正方形OABC的边长为m，和正方形CDEF的边长为n，由此表示出点M、点B和点E的坐标，代入点B的坐标求得求得函数解析式，进一步代入点E，用m表示出n，进一步求得的值即可．

解：设正方形OABC的边长为m，和正方形CDEF的边长为n．

∵点M为OC的中点，

∴点M为（0，）、点B为（m，m）和点E为（n，m+n），

∵抛物线y=ax2+b经过M，B，E三点，

∴m=am2+，

解得：a=，

∴抛物线y=x2+，

把点E（n，m+n）代入抛物线得

m+n=n2+，

解得：n=m+m或n=m﹣m（不合题意，舍去），

即CB=m，EF=m+m，

∴=1+．