题目内容
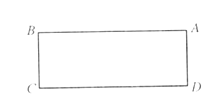
【题目】在边长为a的正方形中挖掉一个边长为b的小正方形（a>b）,把余下的部分剪拼成一个矩形（如图），通过计算图形（阴影部分）的面积，验证了一个等式，则这个等式是（ ）
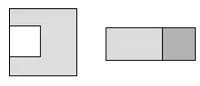
A.a2-b2=（a+b）（a-b）
B.（a+b）2=a2+2ab+b2
C.（a-b）2=a2-2ab+b2
D.a2-ab=a（a-b）
【答案】A
【解析】
已知在左图中，大正方形减小正方形剩下的部分面积为a2b2；因为拼成的长方形的长为（a＋b），宽为（ab），则面积为（a＋b）（ab），根据面积相等，进而得出结论．
解：由图可知，大正方形减小正方形剩下的部分面积为a2b2；
拼成的长方形的面积为：（a＋b）（ab），
所以验证的等式为：a2b2＝（a＋b）（ab），
故选：A．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某商品根据以往销售经验，每天的售价与销售量之间有如下表的关系：
每千克售价（元） | 38 | 37 | 36 | 35 | … | 20 |
每天销售量（千克） | 50 | 52 | 54 | 56 | … | 86 |
设当单价从38元/千克下调到x元时，销售量为y千克，已知y与x之间的函数关系是一次函数．
（1）求y与x的函数解析式；
（2）如果某商品的成本价是20元/千克，为使某一天的利润为780元，那么这一天的销售价应为多少元？（利润=销售总金额﹣成本）
