题目内容
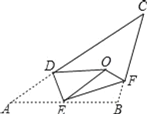
【题目】如图,在□ABCD中,BC=2AB,M是AD的中点,CE⊥AB,垂足为E,求证:∠DME=3∠AEM.

【答案】证明见解析
【解析】
设CM与BA相交于点N,证明△CMD≌△NMA ,得到AN=CD,∠ANM=∠MCD,根据BC=2AB,得到BC=BN,根据等边对等角有∠BNC=∠BCN,根据三角形外角的性质得到∠DME=∠AEM+∠EAM=∠AEM+2∠BNC,根据直角三角形斜边的中线等于斜边的一半得到EM=MN则∠AEM=∠BNC,即可证明.
如图,设CM与BA相交于点N
∵四边形ABCD是平行四边形,M是AD的中点
∴△CMD≌△NMA
∴AN=CD,
∠ANM=∠MCD,
又BC=2AB
∴BC=BN
即∠BNC=∠BCN
又∠EMD是△AEM的外角,∠EAM=∠BCD
∴∠DME=∠AEM+∠EAM
=∠AEM+∠BCD
=∠AEM+∠BCN+∠DCM
=∠AEM+∠BNC+∠DCM
=∠AEM+2∠BNC
又CE⊥AB
∴EM是Rt△CEN中斜边上的中线
∴EM=MN
∴∠AEM=∠BNC
∴∠DME=3∠AEM

练习册系列答案
相关题目
【题目】某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前5名选手的得分如下:
序号 项目 | 1 | 2 | 3 | 4 | 5 |
笔试成绩/分 | 85 | 92 | 84 | 90 | 84 |
面试成绩/分 | 90 | 88 | 86 | 90 | 80 |
根据规定,笔试成绩和面试成绩分别按一定的百分比折和成综合成绩(综合成绩的满分仍为100分)
(1)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(2)求出其余四名选手的综合成绩,并以综合成绩排序确定前两名人选.