��Ŀ����
����Ŀ����ѧϰ��������λ�ߵ�����ʱ��С���Կα������Ľ���취����������˼���� 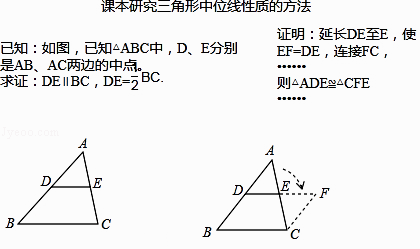 ��������С���ķ��ֽ���������⣺
��������С���ķ��ֽ���������⣺
��1����ͼ1��AD�ǡ�ABC�����ߣ�BE��AC��E����AD��E����AE=EF����֤��AC=BF�� �������С��д�������������������֤���̣�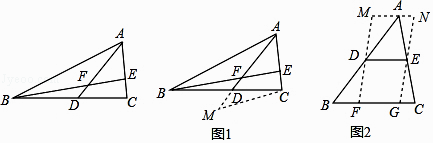
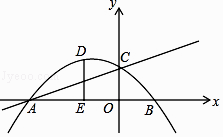
��2��������⣺��ͼ2���ڡ�ABC�У���B=45�㣬AB=10��BC=8��DE�ǡ�ABC����λ�ߣ�����D��E��DF��EG���ֱ�BC��F��G������A��MN��BC���ֱ���FE��GE���ӳ��߽���M��N�����ı���MFGN�ܳ�����Сֵ�� ��
���𰸡�
��1��֤������ͼ1���ӳ�AD����M��ʹMD=FD������MC��
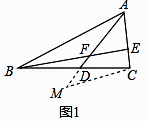
�ڡ�BDF�͡�CDM�У� 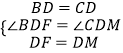 ��
��
���BDF�ա�CDM��SAS����
��MC=BF����M=��BFM��
��EA=EF��
���EAF=��EFA��
�ߡ�AFE=��BFM��
���M=��MAC��
��AC=MC��
��BF=AC
��2��10 ![]() +8
+8
����������2���⣺��ͼ2�� 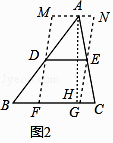
��MN��BC��FM��GN��
���ı���MFGN��ƽ���ı��Σ�
��MF=NG��MN=FG��
��DE�ǡ�ABC����λ�ߣ�
��DE= ![]() BC=4��DE��BC��
BC=4��DE��BC��
��MN=FG= ![]() BC=4��
BC=4��
���ı���MFGN�ܳ�=2��MF+FG��=2MF+8��
��MF��BCʱ��MF��̣�
�����ı���MFGN���ܳ���С��
����A��AH��BC��H��
��FM=AH
��Rt��ABH�У���B=45�㣬AB=10��
��AH= ![]() =5
=5 ![]() ��
��
���ı���MFGN���ܳ���СΪ2MF+8=10 ![]() +8��
+8��
���Դ��ǣ�10 ![]() +8��
+8��
�����㾫����������Ŀ����֪������������������λ�߶��������֪ʶ���Եõ�����Ĵ𰸣���Ҫ�������������������е���߶ν��������ε���λ������������λ�߶����������ε���λ��ƽ���������εĵ����ߣ��ҵ��ڵ����ߵ�һ�룮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�