题目内容
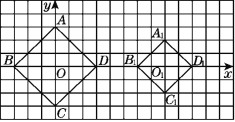
【题目】如图，正方形ABCD和正方形A1B1C1D1的对角线(正方形相对顶点之间所连的线段)BD，B1D1都在x轴上，O，O1分别为正方形ABCD和正方形A1B1C1D1的中心(正方形对角线的交点称为正方形的中心)，O为平面直角坐标系的原点．OD＝3，O1D1＝2.
(1)如果O1在x轴上平移时，正方形A1B1C1D1也随之平移，其形状、大小没有改变，当中心O1在x轴上平移到两个正方形只有一个公共点时，求此时正方形A1B1C1D1各顶点的坐标；
(2)如果O在x轴上平移时，正方形ABCD也随之平移，其形状、大小没有改变，当中心O在x轴上平移到两个正方形公共部分的面积为2个平方单位时，求此时正方形ABCD各顶点的坐标．
【答案】（1）A1(5，2)，B1(3，0)，C1(5，－2)，D1(7，0)；（2）A(11，3)，B(8，0)，C(11，－3)，D(14，0)．
【解析】
（1），两个正方形只有一个公共点时，分D和B1为公共点，B和D1为公共点两种情况，结合平移的性质写出各点的坐标；
（2），根据两个正方形的位置可知公共部分肯定是个正方形，面积是2，可以算出它的对角线长为2，所以有两种情况：点D和O1重合，点B和O1重合，据此解答.
解：(1)当点B1与点D重合时，两个正方形只有一个公共点，此时A1(5，2)，B1(3，0)，C1(5，－2)，D1(7，0)；当点B与D1重合时，两个正方形只有一个公共点，此时A1(－5，2)，B1(－7，0)，C1(－5，－2)，D1(－3，0)．
(2)当点D与O1重合时，两个正方形公共部分的面积为2个平方单位，此时A(5，3)，B(2，0)，C(5，－3)，D(8，0)；当点B与O1重合时，两个正方形公共部分的面积为2个平方单位，此时A(11，3)，B(8，0)，C(11，－3)，D(14，0)．
【题目】丰富的图形世界里有奇妙的数量关系，让我们通过下面这些几何体开始神奇的探索之旅．
观察：下面这些几何体都是简单几何体，请您仔细观察．
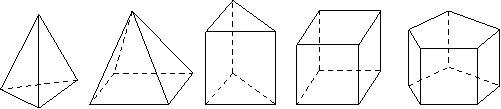
统计：每个几何体都会有棱（棱数为E）、面（面数为F）、顶点（顶点数为V），现将有关数据统计，完成下表．
几何体 | a | b | c | d | e |
棱数（E） | 6 | 9 | 15 | ||
面数（F） | 4 | 5 | 5 | 6 | |
顶点数（V） | 4 | 5 | 8 |
发现：（1）简单几何中，
；
（2）简单几何中，每条棱都是 个面的公共边；
（3）在正方体中，每个顶点处有 条棱，每条棱都有 个顶点，所以有2
3
．
应用：有一个叫“正十二面体”的简单几何体，它有十二个面，每个面都是正五边形，它的每个顶点处都有相同数目的棱．请问它有 条棱， 个顶点，每个顶点处有 条棱．
