题目内容
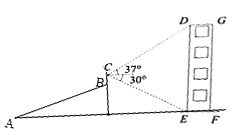
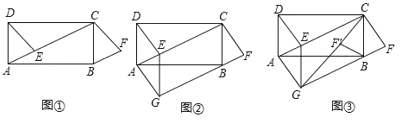
【题目】(操作)如图①,在矩形![]() 中,
中,![]() 为对角线
为对角线![]() 上一点(不与点
上一点(不与点![]() 重合),将
重合),将![]() 沿射线
沿射线![]() 方向平移到
方向平移到![]() 的位置,
的位置,![]() 的对应点为
的对应点为![]() .已知
.已知![]() (不需要证明).
(不需要证明).
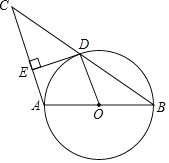
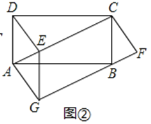
(探究)过图①中的点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() ,其它条件不变,如图②.求证:
,其它条件不变,如图②.求证:![]() .
.
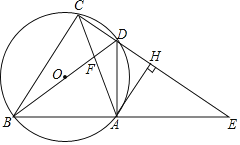
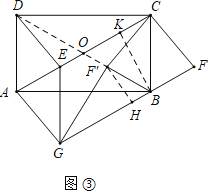
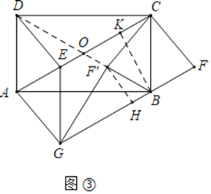
(拓展)将图②中的![]() 沿
沿![]() 翻折得到
翻折得到![]() ,连接
,连接![]() ,其它条件不变,如图③.当
,其它条件不变,如图③.当![]() 最短时,若
最短时,若![]() ,
,![]() ,直接写出
,直接写出![]() 的长和此时四边形
的长和此时四边形![]() 的周长.
的周长.
【答案】探究:见解析;拓展:![]() 四边形
四边形![]() 的周长为
的周长为![]()
【解析】
探究:证明四边形EGBC是平行四边形,推出EG=BC,利用SAS证明三角形全等即可.
拓展:如图3中,连接BD交AC于点O,作BK⊥AC于K,F′H⊥BC于H.由题意四边形AGFC是平行四边形,推出GF=AC=![]() ,由BF=BF′,可以假设BF=x,则BG=
,由BF=BF′,可以假设BF=x,则BG=![]() 利用相似三角形的性质,求出BH,HF′,利用勾股定理求出GF′,再利用二次函数的性质,求出GF′的值最小时BF′的值,推出BF′=
利用相似三角形的性质,求出BH,HF′,利用勾股定理求出GF′,再利用二次函数的性质,求出GF′的值最小时BF′的值,推出BF′=![]() 此时点F′与O重合,由此即可解决问题.
此时点F′与O重合,由此即可解决问题.
解:探究:由平移![]() ,
,![]()
∴![]() ,即
,即![]()
又∵![]() ,∴四边形
,∴四边形![]() 为平行四边形
为平行四边形
∴![]()
∵![]() ,∴∠CBF=∠ACB,
,∴∠CBF=∠ACB,
∵![]()
∴∠AEG=∠ACB,
∴∠AEG=∠CBF
∴![]() .
.
拓展:
如图3中,连接BD交AC于点O,作BK⊥AC于K,F′H⊥BC于H.
∵四边形ABCD是矩形, ∴∠ABC=90°,AB=4,BC=2,
∴![]()
∵![]()
∴![]() ,
,
∴![]()
由题意四边形AGFC是平行四边形, ∴GF=AC=![]() ,
,
∵BF=BF′,可以假设BF=x,则BG=![]()
∵AC∥GF, ∴∠BOK=∠HBF′,
∵∠BKO=∠F′HB=90°,
∴△F′HB∽△BKO,
∴ ![]()
∴ 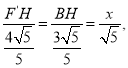
∴![]()
∴![]()
∵ ![]() >0,
>0,
∴当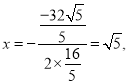 时,GF′的值最小,
时,GF′的值最小,
此时点F′与O重合,由对折得:![]()
由矩形的性质得:![]()
![]()
![]() 四边形BFCF′是菱形,
四边形BFCF′是菱形,
![]() 四边形BFCF′的周长为
四边形BFCF′的周长为![]() ,
,
![]() 且
且![]() 与
与![]() 互相平分,
互相平分,
由勾股定理得:![]()

【题目】我市某校组织“学经典,用经典”知识竞赛,每班参加比赛的学生人数相同,成绩分为![]() 四个等级,其中相应等级的得分依次记为
四个等级,其中相应等级的得分依次记为![]() 分,
分,![]() 分,
分,![]() 分,
分,![]() 分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
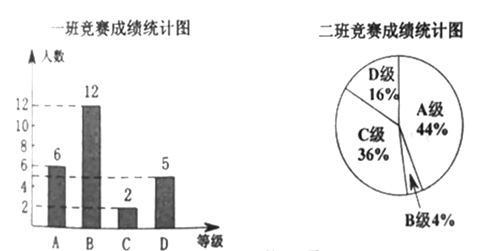
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩“![]() 级”的人数为 ;
级”的人数为 ;
(2)请你将下表补充完整:
平均数(分) | 中位数(分) | 众数(分) | |
一班 |
|
| |
二班 |
|
|
(3)请你对这次两班成绩统计数据的结果进行分析(写出一条结论即可)