题目内容
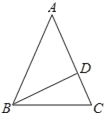
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,则下列结论中①BC=BD=AD;②S△ABD:S△BCD=AD:DC;③BC2=CDAC;④若AB=2,则BC=![]() ﹣1,其中正确的结论的个数是_____个.
﹣1,其中正确的结论的个数是_____个.
【答案】4
【解析】
在△ABC,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,可推出△BCD,△ABD为等腰三角形,可得AD=BD=BC,①正确;由三角形的面积公式得出②正确;利用三角形相似的判定与性质得出③④正确,即可得出结果.
①由AB=AC,∠A=36°,得∠ABC=∠C=72°,
又BD平分∠ABC交AC于点D,
∴∠ABD=∠CBD=![]() ∠ABC=36°=∠A,
∠ABC=36°=∠A,
∴AD=BD,
∠BDC=∠ABD+∠A=72°=∠C,
∴BC=BD,
∴BC=BD=AD,
∴①正确;
②△ABD与△BCD在AC边上的高相等,
故△ABD与△BCD的面积比等于对应底边的比,
∴②正确;
③由①的条件可证△BCD∽△ACB,
则BC:AC=CD:BC,
∴BC2=CDAC,
∴③正确;
④设BC=x,则AC=AB=2,CD=AC﹣AD=2﹣x,
由BC2=CDAC,得x2=(2﹣x)2,
解得x=±![]() ﹣1(舍去负值),
﹣1(舍去负值),
∴BC=![]() ﹣1,
﹣1,
∴④正确.
正确的有4个,
故答案为:4.

练习册系列答案
相关题目