题目内容
【题目】如图,抛物线![]() 经过点
经过点![]() 和点
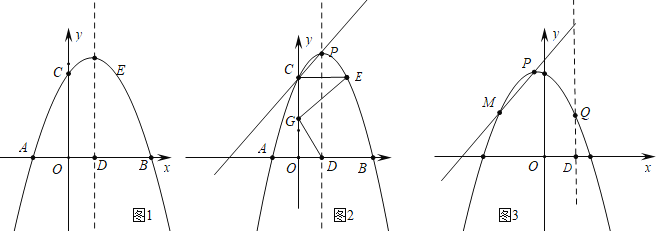
和点![]() ,与y轴交于点C,点P为其顶点,对称轴l与x轴交于点D,抛物线上C、E两点关于对称轴l对称.
,与y轴交于点C,点P为其顶点,对称轴l与x轴交于点D,抛物线上C、E两点关于对称轴l对称.
![]() 求抛物线的函数表达式;
求抛物线的函数表达式;
![]() 点G是线段OC上一动点,是否存在这样的点G,使
点G是线段OC上一动点,是否存在这样的点G,使![]() 与
与![]() 相似,若存在,请求出点G坐标,若不存在请说明理由.
相似,若存在,请求出点G坐标,若不存在请说明理由.
![]() 平移抛物线,其顶点P在直线
平移抛物线,其顶点P在直线![]() 上运动,移动后的抛物线与直线
上运动,移动后的抛物线与直线![]() 的另一交点为M,与原对称轴l交于点Q,当
的另一交点为M,与原对称轴l交于点Q,当![]() 是以PM为直角边的直角三角形时,请写出点Q的坐标.
是以PM为直角边的直角三角形时,请写出点Q的坐标.
【答案】(1)![]() ;(2)G坐标为
;(2)G坐标为![]() 或
或![]() ,见解析;(3)Q的坐标为
,见解析;(3)Q的坐标为![]() 或
或![]() .
.
【解析】
![]() 用两点式表示函数的表达式,即可求解;
用两点式表示函数的表达式,即可求解;
![]() 利用
利用![]() 与
与![]() 相似,则
相似,则![]() ,或
,或![]() ,即可求解;
,即可求解;
![]() 设图象向左平移m个单位,则沿
设图象向左平移m个单位,则沿![]() ,相当于向下同时平移了m个单位,则平移后点
,相当于向下同时平移了m个单位,则平移后点![]() 、点
、点![]() 、
、![]() ,即可求解.
,即可求解.
解:![]() 用两点式表示函数的表达式为:
用两点式表示函数的表达式为:![]() ,
,
令![]() ,则
,则![]() ,函数对称轴为
,函数对称轴为![]() ,则点P坐标为
,则点P坐标为![]() ,点E的坐标
,点E的坐标![]() ;
;
![]() 如图2,设
如图2,设![]() ,则
,则![]() ,
,
![]() 与
与![]() 相似,则
相似,则![]() ,或
,或![]() ,
,
其中![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
将上述数值代入比例关系得:![]() 或2,
或2,
即点G坐标为![]() 或
或![]() ;
;
![]() 设图象向左平移m个单位,则沿
设图象向左平移m个单位,则沿![]() ,相当于向下同时平移了m个单位,
,相当于向下同时平移了m个单位,
则平移后点P坐标![]() ,
,
平移后抛物线的表达式为:![]() ,
,
当![]() 时,
时,![]() ,即点
,即点![]() ,
,
直线表达式为![]() ,
,
联立![]() 并求解得:
并求解得:![]() ,
,
直线PM表达式中的k值为:![]() ,
,
同理直线PQ表达式中的k值为:![]() ,
,
同理直线PM表达式中的k值为:![]() ,
,
![]() 当
当![]() 时,
时,
![]() ,解得:
,解得:![]() ,
,
![]() 当
当![]() 时,
时,
同理可得:![]() ,
,
故点Q的坐标为![]() 或
或![]() .
.

练习册系列答案
相关题目