题目内容
【题目】已知∠A=Rt∠,AB=4,AE=2![]() ,点C在线段AE上运动(不与点A点E重合),过点E作ED⊥BC交BC的延长线于D,则
,点C在线段AE上运动(不与点A点E重合),过点E作ED⊥BC交BC的延长线于D,则![]() 的最大值为( )
的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
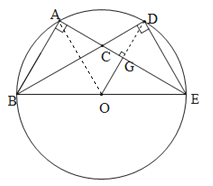
连接BE,作BE的中点O,连接OA、OD.由直角三角形斜边上的中线等于斜边的一半得到OA=OB=OE,OD=OB=OE,从而得到A、B、E、D四点在⊙O上,过O作OG⊥AE于G,延长OG交⊙O于D,则此时DG最大.易证△ABC∽△GDC,得到![]() ,故当DG最大时,
,故当DG最大时,![]() 最大.在Rt△ABE中,利用勾股定理求出BE的长,得到半径的长.由三角形中位线得到OG的长,从而得到DG的最大长度,即可得到结论.
最大.在Rt△ABE中,利用勾股定理求出BE的长,得到半径的长.由三角形中位线得到OG的长,从而得到DG的最大长度,即可得到结论.
连接BE,作BE的中点O,连接OA、OD.
∵∠A=∠BDE=90°,AO是Rt△ABE斜边上的中线,∴OA=OB=OE,同理OD=OB=OE,∴A、B、E、D四点在⊙O上,过O作OG⊥AE于G,延长OG交⊙O于D,则此时DG最大.
∵∠A=90°,∴∠A=∠DGC=90°.
∵∠ACB=∠DCG,∴△ABC∽△GDC,∴![]() ,∴当DG最大时,
,∴当DG最大时,![]() 最大.
最大.
∵BE=![]() =10,∴OB=OE=OD=5.
=10,∴OB=OE=OD=5.
∵OG⊥AE,∴AG=GE.
∵BO=EO,∴OG为△ABE的中位线,∴OG=![]() AB=2,∴DG=OD-OG=5-2=3,∴
AB=2,∴DG=OD-OG=5-2=3,∴![]() .
.
故选C.

练习册系列答案
相关题目