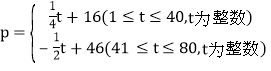题目内容
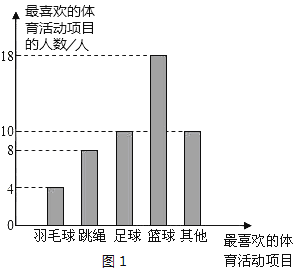
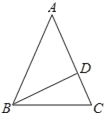
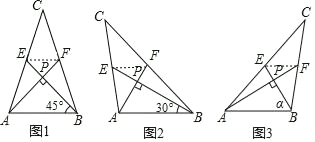
【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P.像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
特例探索
(1)①如图1,当∠ABE=45°,c=2![]() 时,a= ,b= ;
时,a= ,b= ;
②如图2,当∠ABE=30°,c=4时,求a和b的值.
归纳证明
(2)请你观察(1)中的计算结果,猜想三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
(3)利用(2)中的结论,解答下列问题:
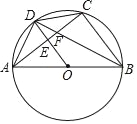
在边长为3的菱形ABCD中,O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图4所示,求MG2+MH2的值.
【答案】(1)①2![]() ,2
,2![]() ;② a=2
;② a=2![]() ,b=2
,b=2![]() ;(2)关系为:a2+b2=5c2,证明见解析;(3)5.
;(2)关系为:a2+b2=5c2,证明见解析;(3)5.
【解析】
(1)在图1中,PB=ABsin45°=2=PA,即可求解;同理可得:a=2![]() ,b=2
,b=2![]() ;
;
(2)PB=ABcosα=ccosα,PA=csinα,PF=![]() PA=
PA=![]() csinα,PE=
csinα,PE=![]() csinα,则a2+b2=(2AE)2+(2BF)2,即可求解;
csinα,则a2+b2=(2AE)2+(2BF)2,即可求解;
(3)证明:MG=![]() ME=
ME=![]() MB,MH=
MB,MH=![]() MC,则MG2+MH2=
MC,则MG2+MH2=![]() (MB2+MC2),即可求解.
(MB2+MC2),即可求解.
解:如图1、2、3、4,连接EF,则EF是△ABC的中位线,
则EF=AB,EF∥AB,∴△EFP∽△BPA,
∴![]() …①,
…①,
(1)在图1中,PB=ABsin45°=2=PA,
由①得:PF=1,
b=2BF=2![]() =2
=2![]() =a;
=a;
②同理可得:a=2![]() ,b=2
,b=2![]() ;
;
(2)关系为:a2+b2=5c2,
证明:如图3,设:∠EAB=α,
则:PB=ABcosα=ccosα,PA=csinα,
由①得:PF=![]() PA=
PA=![]() csinα,PE=
csinα,PE=![]() csinα,
csinα,
则a2+b2=(2AE)2+(2BF)2=c2×5[(sinα)2+(cosα)2]=5c2;
(3)∵AE=OE=![]() EC,AG∥BC,
EC,AG∥BC,
∴AG=![]() BC=
BC=![]() AD,则EF=
AD,则EF=![]() BC=
BC=![]() AD,
AD,
同理HG=![]() AD,∴GH=
AD,∴GH=![]() AD,
AD,
∴GH=![]() EF,
EF,
∵GH∥BC,EF∥BC,
∴HG∥EF,∴MG=![]() ME=
ME=![]() MB,
MB,
同理:MH=![]() MC,
MC,
则MG2+MH2=![]() (MB2+MC2)=
(MB2+MC2)=![]() ×5×BC2=5.
×5×BC2=5.