题目内容
【题目】如图，点M为双曲线y＝
上一点，过点M作x轴、y轴的垂线，分别交直线y＝﹣x+2m于D、C两点，若直线y＝﹣x+2m交y轴于A，交x轴于B，则ADBC的值为_____．
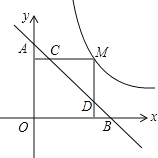
【答案】2
【解析】
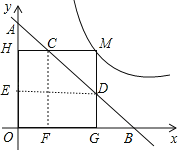
如图，过点M作x轴、y轴的垂线，垂足分别为G、H，作DE⊥y轴于E，CF⊥x轴于F，先证明△OAB为等腰直角三角形，则判断△AED和△BCF都为等腰直角三角形，所以AD=
DE，BC=CF，则ADBC=2DECF，设M(x，y)，利用反比例函数图象上点的坐标特征得到xy=1，从而得到ADBC的值．
如图，过点M作x轴、y轴的垂线，垂足分别为G、H，作DE⊥y轴于E，CF⊥x轴于F，
当x=0时，
，则A(0，
)，
当y=0时，
，解得x=m，则B(，0)，
∴OA=OB=，
∴△OAB为等腰直角三角形，
∵DE⊥y轴，CF⊥x轴，
∴△AED和△BCF都为等腰直角三角形，
∴AD=DE，BC=CF，
∴ADBC=2DECF，
设M(x，y)，
∴DE=MH=x，CF=MG=y，
∴ADBC=2xy=2×1=2．
故答案为：2．
练习册系列答案
相关题目
