��Ŀ����
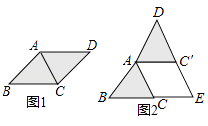
����Ŀ��С����С����ѧϰ̽��������ȫ��ʱ����������һ�⣺��ͼ������AC��AD��BC��BD������ACB����ADB�������Ĺ�ϵ��

(1)��������ǽ�𣬲�˵�����ɣ�
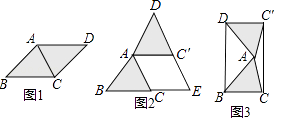
(2)ϸ�ĵ�С���ڽ��Ĺ����У����������AB����ȡһ��E������CE��DE������CE��DE����֪��Ϊʲô��(��ͼ��)?
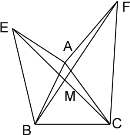
(3)С����С��˵�����ɺ���������AB���ӳ�������ȡһ��P��Ҳ��(2)�����ƵĽ��ۣ����������ͼ���л���ͼ�Σ���д�����ۣ���Ҫ��˵�����ɣ�
���𰸡���1������������2������������3��PC=PD��ͼ�μ�����
��������
��1������ȫ�������ε��ж�����SSS֤����ACB�ա�ADB��
��2���ɣ�1���е�ȫ����������ACB�ա�ADB�Ķ�Ӧ�����������CAE=��DAE������ȫ�������ε��ж�����SAS֤����CAE�ա�DAE�����Ӧ��CE=DE��
��3��ͬ��2��������ȫ�������εĶ�Ӧ�����֤�ý��ۣ�
��1���⣺��ACB�ա�ADB���������£�
��ͼ1��������ACB����ADB�У�
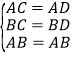 ��
��
���ACB�ա�ADB��SSS����
��2���⣺��ͼ2�����ɣ�1��֪����ACB�ա�ADB��
���CAB=��DAB������CAE=��DAE��
����CAE����DAE��
 ��
��
���CAE�ա�DAE��SAS����
��CE=DE��
��3���⣺��ͼ3��PC=PD.
����ͬ��2������APC�ա�APD��SAS����
��PC=PD.