题目内容
【题目】如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连接BE、CE.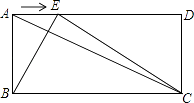
若a=5,sin∠ACB= ![]() ,解答下列问题:
,解答下列问题:
(1)填空:b=;
(2)当BE⊥AC时,求出此时AE的长;
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,请写x、a、b三者的关系式.
【答案】
(1)12
(2)
解:∵BE⊥AC,
∴∠EBC+∠ACB=90°
又∵∠ABE+∠EBC=90°,
∴∠ABE=∠ACB,
又∵∠BAE=∠ABC=90°,
∴△AEB∽△BAC,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴AE= ![]()
(3)
解:∵点E在线段AD上的任一点,且不与A、D重合,
∴当△ABE与△BCE相似时,则∠BEC=90°,
①当△ABE∽△EBC时,∠ABE=∠EBC=45°,
∴△EBC是等腰直角三角形,
BC= ![]() BE,BE=
BE,BE= ![]() AB,
AB,
∴BC=2AB,即b=2a,x=a或x= ![]() b.
b.
②当△BAE∽△CEB
∴∠ABE=∠BCE,
又∵BC∥AD,
∴∠DEC=∠BCE,
∴∠ABE=∠DEC,
又∵∠BAE=∠EDC=90°,
∴△BAE∽△EDC,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴x2﹣bx+a2=0,
即(x﹣ ![]() )2=
)2= ![]() ,
,
当b2﹣4a2≥0,
∵a>0,b>0,
∴b≥2a,
即b≥2a时,x= ![]() .
.
综上所述:当a、b满足条件b=2a时△BAE∽△CEB,此时x= ![]() b(或x=a);当a、b满足条件b>2a时△BAE∽△CEB,此时x=
b(或x=a);当a、b满足条件b>2a时△BAE∽△CEB,此时x= ![]() .
.

【解析】解:(1)∵在矩形ABCD中,
∴∠ABC=90°,
∵AB=a=5,sin∠ACB= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AC=13,
∴BC= ![]() =12,
=12,
∴b=12;
所以答案是:12;
【考点精析】利用相似三角形的性质和相似三角形的判定对题目进行判断即可得到答案,需要熟知对应角相等,对应边成比例的两个三角形叫做相似三角形;相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).

 阅读快车系列答案
阅读快车系列答案【题目】抛物线y=ax2+bx+c上,部分点的横、纵坐标x、y的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | ﹣4 | ﹣4 | 0 | 8 |
(1)根据上表填空; ①方程ax2+bx+c=0的两个根分别是和 .
②抛物线经过点(﹣3,);
③在对称轴左侧,y随x增大而;
(2)求抛物线y=ax2+bx+c的解析式.