题目内容
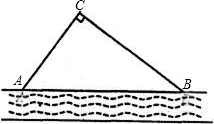
某校把一块沿河的三角形废地(如图)开辟为生物园,已知∠ACB=90°,
∠CAB=54°,BC=60米.
1.现学校准备从点C处向河岸AB修一条小路CD,使得CD将生物园分割成面积相等的两部分.请你用直尺和圆规在图中作出小路CD(保留作图痕迹);
2.为便于浇灌,学校在点C处建了一个蓄水池,利用管道从河中取水.已知每铺设1米管道费用为50元,求铺设管道的最低费用.(sin36°≈0.588,cos36°≈0.809,tan36°≈0.727,精确到1元)

1.用尺规作AB的垂直平分线交AB于点D,连接CD. …………………3分
2.作CE⊥AB. ∵∠ACB=90°,∠CAB=54°
∴ ∠ABC=36° ………………………………4分
在Rt△BCE中,![]() =sin∠CBE. …………………………6分
=sin∠CBE. …………………………6分
∴CE=BC·sin∠CBE=60·sin36°≈35.28(米) ……………………8分
∴铺设管道的最低费用=50·CE≈1764(元) ………………………9分
解析:(1)若让CD将生物园分割成面积相等的两部分,则高相等,只需底相等,利用垂直平分线的做法即可.
(2)作高CE. 由∠CAB=54°得∠ABC=36°. 在Rt△BCE中,=sin∠CBE.
∴CE=BC·sin∠CBE=60·sin36°≈35.28(米).即铺设管道的最低费用=50·CE≈1764(元)

练习册系列答案
相关题目
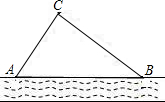
 AB=54°,BC=60米.
AB=54°,BC=60米.
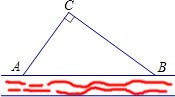 (2011•包河区一模)某校把一块沿河的三角形废地(如图)开辟为生物园(设AB段河岸为直线型),已知∠ACB=90°,∠CAB=54°,BC=60米.为便于浇灌,学校在点C处建一个蓄水池,利用管道从河中取水.已知每铺设1米管道费用为50元,求铺设管道的最低费用(精确到1元).(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38)
(2011•包河区一模)某校把一块沿河的三角形废地(如图)开辟为生物园(设AB段河岸为直线型),已知∠ACB=90°,∠CAB=54°,BC=60米.为便于浇灌,学校在点C处建一个蓄水池,利用管道从河中取水.已知每铺设1米管道费用为50元,求铺设管道的最低费用(精确到1元).(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38)