题目内容
【题目】已知,如图,二次函数![]() (
(![]() )图象的顶点为
)图象的顶点为![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 点右侧),点
点右侧),点![]() ,
,![]() 关于直线
关于直线![]() 对称.
对称.
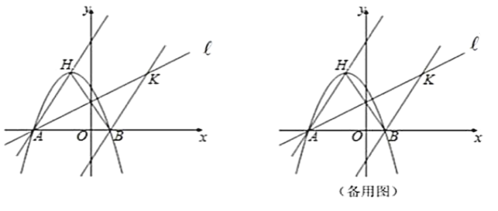
(1)![]() 坐标为 ;
坐标为 ;![]() 坐标为: ;
坐标为: ;![]() 坐标为 ;
坐标为 ;
(2)求二次函数解析式;
(3)在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 最大?若不存在,请说明理由:若存在,请求出此时
最大?若不存在,请说明理由:若存在,请求出此时![]() 的面积;
的面积;
(4)过点![]() 作直线
作直线![]() 交直线
交直线![]() 于
于![]() 点,
点,![]() ,
,![]() 分别为直线
分别为直线![]() 和直线
和直线![]() 上的两个动点,连接
上的两个动点,连接![]() 、
、![]() 、
、![]() ,求
,求![]() 和的最小值.
和的最小值.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() 的面积为
的面积为![]() ;(4)
;(4)![]() 的最小值为8.
的最小值为8.
【解析】
(1)由直线的解析式可求出点A的坐标;再根据二次函数的对称轴可知点B的坐标;然后根据直线的解析式和点![]() 、
、![]() 的横坐标确定HB与直线的交点在y轴上,最后根据点的对称性求解即可;
的横坐标确定HB与直线的交点在y轴上,最后根据点的对称性求解即可;
(2)将点H的坐标代入二次函数的解析式求解即可;
(3)先根据三角形的三边关系确定点P的位置,再求出其坐标,最后根据三角形的面积公式求解即可;
(4)先求出点K的坐标,再利用两点之间线段最短求出![]() 的最小值为BM,然后再次利用两点之间线段最短求出
的最小值为BM,然后再次利用两点之间线段最短求出![]() 的最小值,即为
的最小值,即为![]() 最小值,最后利用勾股定理求解即可.
最小值,最后利用勾股定理求解即可.
(1)令![]() ,代入直线的解析式得:
,代入直线的解析式得:![]()
解得:![]() ,则点A的坐标为
,则点A的坐标为![]()
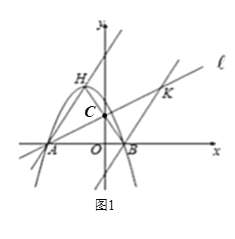
如图1,设直线与y轴的交点为C
令![]() ,代入直线的解析式得:
,代入直线的解析式得:![]() ,则点C的坐标为
,则点C的坐标为![]()
二次函数![]() 的对称轴为
的对称轴为![]() ,点A、B关于对称轴对称
,点A、B关于对称轴对称
则点B的坐标为![]() ,二次函数顶点D的横坐标为
,二次函数顶点D的横坐标为![]()
点![]() 、
、![]() 关于直线
关于直线![]() 对称,并且点
对称,并且点![]() 、
、![]() 的横坐标关于原点对称
的横坐标关于原点对称
则HB与直线![]() 的交点为点
的交点为点![]()
因此,点H的纵坐标为![]() ,即点H的坐标为
,即点H的坐标为![]()
综上,![]() ;
;
(2)把![]() 代入
代入![]() 得:
得:![]()
解得:![]()
故二次函数解析式为![]() ;
;
(3)由三角形的三边关系得:![]()
则当P、H、A三点共线时,![]() 最大,最大值为AH
最大,最大值为AH
此时,点P为直线![]() 与AH所在直线的交点
与AH所在直线的交点
设直线![]() 的解析式为
的解析式为![]()
将![]() 和
和![]() 代入得:
代入得: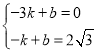
解得: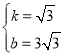 ,则直线AH的解析式为
,则直线AH的解析式为![]()
联立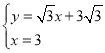 ,解得
,解得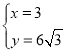
则点P的坐标为![]() ;
;
故此时![]() 的面积为
的面积为![]()
综上,存在这样的点P,使得![]() 最大,此时
最大,此时![]() 的面积为
的面积为![]() ;
;
(4)∵过点![]() 作直线
作直线![]() ,直线AH的解析式为
,直线AH的解析式为![]()
∴直线![]() 的解析式为
的解析式为![]() 中的
中的![]()
又因为![]() 在直线
在直线![]() 上,代入求出
上,代入求出![]()
∴直线![]() 的析解式为:
的析解式为:![]()
联立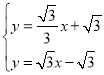 ,解得:
,解得: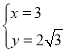
∴交点![]() 的坐标是
的坐标是![]()
则![]()
∵点![]() 、
、![]() 关于直线
关于直线![]() 对称
对称
∴![]() 的最小值是
的最小值是![]()
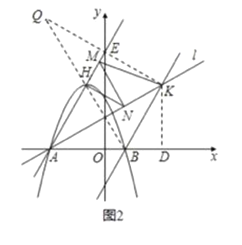
如图2,过![]() 作
作![]() 轴于
轴于![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,交直线
,交直线![]() 于
于![]()
则![]() ,
,![]() ,
,![]() ,
,![]()
![]()
∴根据两点之间线段最短公理得出![]() 的最小值是
的最小值是![]()
即![]() 的长是
的长是![]() 的最小值
的最小值
∵![]()
∴![]()
由勾股定理得![]()
故![]() 的最小值为8.
的最小值为8.

【题目】某超市销售一种商品,成本每千克30元,规定每千克售价不低于成本,且不高于70元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 40 | 50 | 60 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
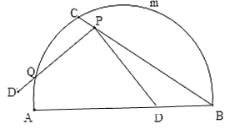
【题目】如图,C是![]() 的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转
的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转![]() 得到线段
得到线段![]() .射线
.射线![]() 与
与![]() 交于点Q.已知
交于点Q.已知![]() ,设P,C两点间的距离为xcm,P,D两点间的距离
,设P,C两点间的距离为xcm,P,D两点间的距离![]() ,P,Q两点的距离为
,P,Q两点的距离为![]() .
.
小石根据学习函数的经验,分别对函数![]() ,
,![]() ,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() ,与x的几组对应值:
,与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4.29 | 3.33 | 1.65 | 1.22 | 1.0 | 2.24 | |
| 0.88 | 2.84 | 3.57 | 4.04 | 4.17 | 3.20 | 0.98 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数据所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
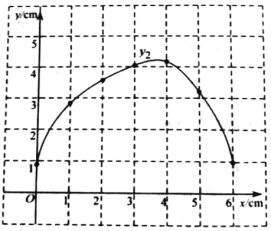
(3)结合函数图象,解决问题:连接DQ,当△DPQ为等腰三角形时,PC的长度约为_____cm.(结果保留一位小数)