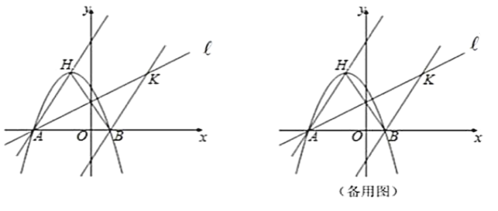题目内容
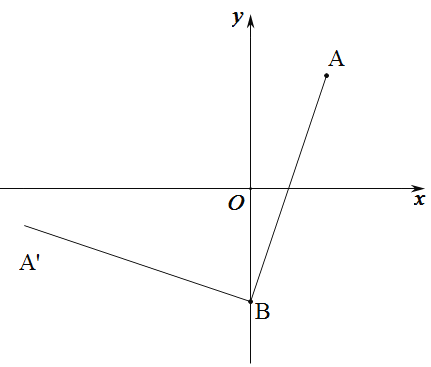
【题目】如图，A点坐标为
，B点坐标为
，将线段AB绕点B逆时针旋转90°，得到线段
B，则点坐标为_______.
【答案】
【解析】
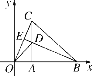
过点A作AD⊥y轴于D，过点A＇作A＇E⊥y轴于E，根据点A、B的坐标表示出BD、AD，再求出△ABD和△BA＇E全等，根据全等三角形对应边相等可得AD=BE=2，BD= A＇E=6，然后表示出OE，再写出点A＇的坐标即可．
解：（1）如图，
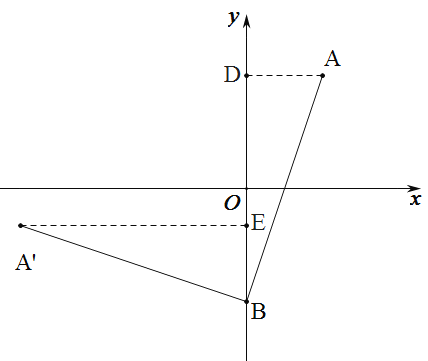
过点A作AD⊥y轴于D，过点A＇作A＇E⊥y轴于E，
∴∠ADB=∠BEA＇=90°，
∴∠BAD+∠ABD=90°，
由旋转知，AB=A＇B，∠ABA＇=90°，
∴∠ABD+∠A＇BE=90°，
∴∠BAD=∠A＇BE，
在△ABD和△BA＇E中，
，
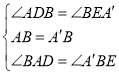∴△ABD≌△BA＇E，
∴BD=A＇E，AD=BE，
∵A（2，3），B（0，-3），
∴AD=BE=2，BD= A＇E =6，
∴OE=OB-BE=3-2=1，
∴A＇（-6，-1）；
练习册系列答案
字词句段篇系列答案
相关题目
