题目内容
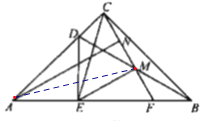
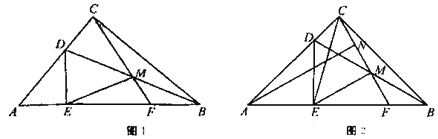
【题目】如图1,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E,点M为BD中点,CM的延长线交AB于点F.
(1)求证:CM=EM;
(2)若∠BAC=50°,求∠EMF的大小;
(3)如图2,若△DAE≌△CEM,点N为CM的中点,求证:AN∥EM.
【答案】(1)证明见解析;(2)∠EMF=100°;(3)证明见解析.
【解析】(1)在Rt△DCB和Rt△DEB中,利用直角三角形斜边中线等于斜边一半进行证明即可得;
(2)根据直角三角形两锐角互余可得∠ABC=40°,根据CM=MB,可得∠MCB=∠CBM,从而可得∠CMD=2∠CBM,继而可得∠CME=2∠CBA=80°,根据邻补角的定义即可求得∠EMF的度数;
(3)由△DAE≌△CEM,CM=EM,∠DEA=90°,结合CM=DM以及已知条件可得△DEM是等边三角形,从而可得∠EDM=60°,∠MBE=30°,继而可得∠ACM=75°,连接AM,结合AE=EM=MB,可推导得出AC=AM,根据N为CM中点,可得AN⊥CM,再根据CM⊥EM,即可得出AN∥EM.
(1)∵M为BD中点,
Rt△DCB中,MC=![]() BD,
BD,
Rt△DEB中,EM=![]() BD,
BD,
∴MC=ME;
(2)∵∠BAC=50°,∠ACB=90°,
∴∠ABC=90°-50°=40°,
∵CM=MB,
∴∠MCB=∠CBM,
∴∠CMD=∠MCB+∠CBM=2∠CBM,
同理,∠DME=2∠EBM,
∴∠CME=2∠CBA=80°,
∴∠EMF=180°-80°=100°;
(3)∵△DAE≌△CEM,CM=EM,
∴AE=EM,DE=CM,∠CME=∠DEA=90°,∠ECM=∠ADE,
∵CM=EM,∴AE=ED,∴∠DAE=∠ADE=45°,
∴∠ABC=45°,∠ECM=45°,
又∵CM=ME=![]() BD=DM,
BD=DM,
∴DE=EM=DM,
∴△DEM是等边三角形,
∴∠EDM=60°,
∴∠MBE=30°,
∵CM=BM,∴∠BCM=∠CBM,
∵∠MCB+∠ACE=45°,
∠CBM+∠MBE=45°,
∴∠ACE=∠MBE=30°,
∴∠ACM=∠ACE+∠ECM=75°,
连接AM,∵AE=EM=MB,
∴∠MEB=∠EBM=30°,
∠AME=![]() ∠MEB=15°,
∠MEB=15°,
∵∠CME=90°,
∴∠CMA=90°-15°=75°=∠ACM,
∴AC=AM,
∵N为CM中点,
∴AN⊥CM,
∵CM⊥EM,
∴AN∥CM.