��Ŀ����
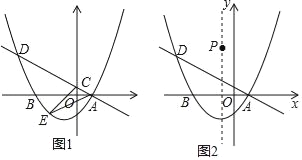
����Ŀ����֪��ֱ��AB��DC����PΪƽ����һ�㣬����AP��CP��



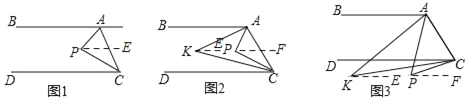
��1����ͼ1����P��ֱ��AB��CD֮�䣬����BAP=60�㣬��DCP=20��ʱ�����APC��
��2����ͼ2����P��ֱ��AB��CD֮�䣬��BAP���DCP�Ľ�ƽ�����ཻ�ڵ�K��д����AKC���APC֮���������ϵ����˵�����ɣ�
��3����ͼ3����P����CD�⣬��BAP���DCP�Ľ�ƽ�����ཻ�ڵ�K����AKC���APC�к�������ϵ����˵�����ɣ�
���𰸡���1��80�㣻��2������������3��������
�����������������
�ֱ����P��K��AB��ƽ���ߣ�����ƽ���ߵ����ʺͽ�ƽ���ߵĶ��弴�����.
�⣺��1����ͼ1����P��PE��AB��
��AB��CD��
��PE��AB��CD��
���APE=��BAP����CPE=��DCP��
���APC=��APE+��CPE=��BAP+��DCP=60��+20��=80�㣻
��2����AKC=![]() ��APC��
��APC��
���ɣ���ͼ2����K��KE��AB��
��AB��CD��
��KE��AB��CD��
���AKE=��BAK����CKE=��DCK��
���AKC=��AKE+��CKE=��BAK+��DCK��
��P��PF��AB��
ͬ���ɵã���APC=��BAP+��DCP��
�ߡ�BAP���DCP�Ľ�ƽ�����ཻ�ڵ�K��
���BAK+��DCK=![]() ��BAP+
��BAP+![]() ��DCP=
��DCP=![]() ����BAP+��DCP��=
����BAP+��DCP��=![]() ��APC��
��APC��
���AKC=![]() ��APC��
��APC��
��3����AKC=![]() ��APC��
��APC��
���ɣ���ͼ3����K��KE��AB��
��AB��CD��
��KE��AB��CD��
���BAK=��AKE����DCK=��CKE��
���AKC=��AKE����CKE=��BAK����DCK��
��P��PF��AB��
ͬ���ɵã���APC=��BAP����DCP��
�ߡ�BAP���DCP�Ľ�ƽ�����ཻ�ڵ�K��
���BAK����DCK=![]() ��BAP��
��BAP��![]() ��DCP=
��DCP=![]() ����BAP����DCP��=
����BAP����DCP��=![]() ��APC��
��APC��
���AKC=![]() ��APC��
��APC��

 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�