题目内容
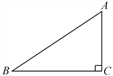
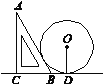
【题目】如图,一块直角三角板ABC(∠A=30°)的斜边AB与一个以r为半径的圆轮子相靠,若BD=1,则r等于( )
A. 2 B. ![]() C. 1.5 D.
C. 1.5 D. ![]()
【答案】B
【解析】记⊙O与直角三角尺的斜边切于点E,连结OB,OE,由已知可求出∠ABC的度数,进而可求出∠ABD的度数,由已知不难证得△OEB≌△ODB,再利用全等三角形的性质,结合直角三角形的两个锐角互余,求出∠OBD、∠BOD的度数,在Rt△ODB中,由特殊角所对的直角边与斜边的关系,利用直角三角形的勾股定理即可求解.
记⊙O与△ABC切于点E,连结OE、OB.
∵ 在Rt△ACB中,∠C=90°,∠A=30°
∴ ∠ABC=60° (直角三角形的两个锐角互余)
∵ ∠ABC+∠ABD=180°,∠ABC=60°,
∴ ∠ABD=120°,
∵ AB、BD与⊙O分别相切于点E、D.
∴ OE⊥AB OD⊥BD (过切点及圆心的线段垂直于该切线)
∴ △OEB和△ODB是直角三角形 (两边相互垂直的三角形是直角三角形)
∵ BE、BD是过点B的⊙O的两条切线,
∴ BE=BD (切线长定理)
∵ BE=BD OB=OB
∴ Rt△OEB≌Rt△ODB (HL)
∴ ∠OBE=∠OBD (全等三角形的对应角相等)
∵ ∠ABD=120° ,∠OBE=∠OBD
∴ ∠OBE=∠OBD=60°
∵ ∠ODB=90° ,∠OBD=60°
∴ ∠BOD=30° (直角三角形的两个锐角互余)
∵ ∠ODB=90° ,BOD=30°
∴ BD=![]() ×OB (在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半)
×OB (在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半)
∵ BD=BD=![]() ×OB
×OB
∴ OB=2,
∵ ∠ODB=90° ,BD=1,OB=2,
∴ OD=![]() (直角三角形勾股定理求值)
(直角三角形勾股定理求值)
即r=![]()
故选:B.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案