题目内容
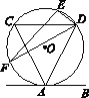
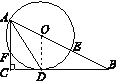
【题目】如图,在Rt△ABC中,∠C=90°,O,D分别为AB,BC上的点,经过A,D两点的⊙O分别交AB,AC于点E,F,且D为弧EF的中点.
(1)求证:BC与⊙O相切;
(2)当⊙O的半径r=2,∠CAD=30°时,求劣弧AD的长.

【答案】(1)见解析;(2)![]()
【解析】(1)连接OD.欲证明BC与 O相切,只要证明BC⊥OD即可;
(2)由同弧所对的圆周角相等可以推知∠OAD=∠ODA=∠CAD=30°;可得∠AOD=120°,由弧长的计算公式求解即可.
(1)如图,连结OD,则OD=OA,
∴∠OAD=∠ODA(等边对等角).
∵![]() ,
,
∴∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD∥AC.
∵∠C=90°,
∴∠ODC=90°,即BC⊥OD,
∴BC与⊙O相切;
(2)∵∠OAD=∠ODA=∠CAD=30°,
∴∠AOD=120°.
∵⊙O的半径r=2,
∴劣弧AD的长为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目