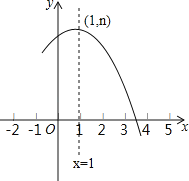题目内容
【题目】阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫做该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=﹣x+4.问题与探究:如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A,C分别在x轴和y轴上,抛物线y=![]() (x﹣a)2+b经过B,C两点,顶点D在正方形内部.若点D有一条特征线是y=x+2,则此抛物线的表达式是_____.
(x﹣a)2+b经过B,C两点,顶点D在正方形内部.若点D有一条特征线是y=x+2,则此抛物线的表达式是_____.
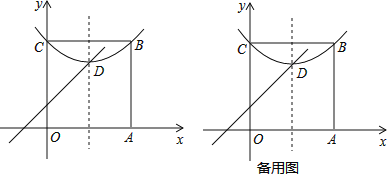
【答案】y=![]() (x-4)2+6
(x-4)2+6
【解析】
由特征线确定a与b的关系为b=a+2,再有D点横坐标,确定正方形边长为2a,进而得到C(0,2a),将C点坐标代入函数解析式即可求得a.
由题意可知D(a,b)在y=x+2上,
∴b=a+2,
∴正方形的边长为2a,
∴C(0,2a),
将点C代入y=![]() (x﹣a)2+b得到,
(x﹣a)2+b得到,
![]() (﹣a)2+a+2=2a,
(﹣a)2+a+2=2a,
∴a1=a2=4
∴y=![]() (x-4)2+6;
(x-4)2+6;
故答案为y=![]() (x-4)2+6.
(x-4)2+6.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目