ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΘ®1Θ©–ΓMyΆ§―ß‘ΎΆχ¬γ÷±≤ΞΩΈ÷–―ßœΑΝΥΙ¥Ι…Ε®άμΘ§ΥϊœκΑ―’β“Μ÷Σ Ε”Π”Ο‘ΎΒ»±Ώ»ΐΫ«–Έ÷–ΘΚ±Ώ≥ΛΈΣaΒΡΒ»±Ώ»ΐΫ«–ΈΟφΜΐ «ΓΓ ΓΓΘ®”ΟΚ§aΒΡ¥ζ ΐ Ϋ±μ ΨΘ©ΘΜ
Θ®2Θ©–ΓMyΆ§―ßΫχ“Μ≤ΫΥΦΩΦΘΚ «ΖώΩ…“‘ΫΪ’ΐΖΫ–ΈΦτΤ¥≥…“ΜΗωΒ»±Ώ»ΐΫ«–ΈΘ®≤Μ÷ΊΒΰΓΔΈόΖλœΕΘ©ΘΩ
ΔΌ»γΙϊΫΪ“ΜΗω±Ώ≥ΛΈΣ2ΒΡ’ΐΖΫ–Έ÷ΫΤ§ΦτΤ¥Β»±Ώ»ΐΫ«–ΈΘ§Ρ«Ο¥ΗΟ»ΐΫ«–Έ±Ώ≥ΛΒΡΤΫΖΫ «ΓΓ ΓΓΘΜ
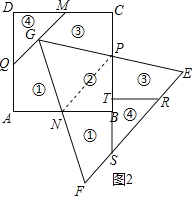
ΔΎ–ΓMyΆ§―ßΑ¥œ¬ΆΦ«–ΗνΖΫΖ®ΫΪ’ΐΖΫ–ΈABCDΦτΤ¥≥…“ΜΗωΒ»±Ώ»ΐΫ«–ΈEFGΘΚMΓΔNΖ÷±πΈΣABΓΔCD±Ώ…œΒΡ÷–ΒψΘ§PΓΔQ «±ΏBCΓΔAD…œΝΫΒψΘ§GΈΣMQ…œ“ΜΒψΘ§«“ΓœMGPΘΫΓœPGNΘΫΓœNGQΘΫ60ΓψΘ°
«κ≤Ι»ΪΆΦ–ΈΘ§Μ≠≥ωΤ¥≥…’ΐ»ΐΫ«–ΈΒΡΗς≤ΩΖ÷Ζ÷ΗνœΏΘ§≤Δ±ξΚ≈ΘΜ
Δέ’ΐΖΫ–ΈABCDΒΡ±Ώ≥ΛΈΣ2Θ§…ηBPΘΫxΘ§‘ρx2ΘΫΓΓ ΓΓΘ°

ΓΨ¥πΑΗΓΩΘ®1Θ©![]() a2ΘΜΘ®2Θ©ΔΌ
a2ΘΜΘ®2Θ©ΔΌ![]() ΘΜΔΎœξΦϊΫβΈωΘΜΔέ
ΘΜΔΎœξΦϊΫβΈωΘΜΔέ![]() ©¹1Θ°
©¹1Θ°
ΓΨΫβΈωΓΩ
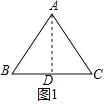
Θ®1Θ©»γΆΦ1Θ§ΙΐAΉςADΓΆBC”ΎDΘ§ΗυΨίΒ»±Ώ»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫBDΘΫCDΘΫ![]() BCΘΫ
BCΘΫ![]() aΘ§”…Ι¥Ι…Ε®άμΒΟΒΫADΘΫ
aΘ§”…Ι¥Ι…Ε®άμΒΟΒΫADΘΫ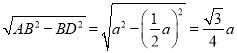 Θ§”Ύ «ΒΟΒΫSΓςABCΘΫ
Θ§”Ύ «ΒΟΒΫSΓςABCΘΫ![]() BCADΘΫ
BCADΘΫ![]() ΘΜ
ΘΜ
Θ®2Θ©ΔΌΗυΨί»ΐΫ«–ΈΒΡΟφΜΐΙΪ ΫΦ¥Ω…ΒΟΒΫΫα¬έΘΜ
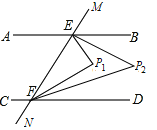
ΔΎ≤Ι»ΪΆΦ–Έ»γΆΦ2Υυ ΨΘΜ
Δέ”…Χβ“β÷ΣΘ§PGΘΫPEΘ§GNΘΫNFΘ§ΆΤ≥ωPN «ΓςGEFΒΡ÷–ΈΜœΏΘ§ΒΟΒΫPNΘΫ![]() EFΘ§ΗυΨίΙ¥Ι…Ε®άμΦ¥Ω…ΒΟΒΫΫα¬έΘ°
EFΘ§ΗυΨίΙ¥Ι…Ε®άμΦ¥Ω…ΒΟΒΫΫα¬έΘ°
ΫβΘΚΘ®1Θ©»γΆΦΘ§ΙΐAΉςADΓΆBC”ΎDΘ§
ΓΏΓςABC «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύBDΘΫCDΘΫ![]() BCΘΫ
BCΘΫ![]() aΘ§
aȧ
ΓύADΘΫ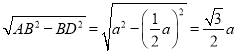 Θ§
Θ§
ΓύSΓςABCΘΫ![]() BCADΘΫ
BCADΘΫ![]() a2ΘΜ
a2ΘΜ
Θ®2Θ©ΔΌΓΏ±Ώ≥ΛΈΣ2ΒΡ’ΐΖΫ–ΈΒΡΟφΜΐΘΫ4Θ§
ΓύΦτΤ¥≥…ΒΡΒ»±Ώ»ΐΫ«–ΈΒΡΟφΜΐΘΫ4Θ§
Γύ![]() a2ΘΫ4Θ§
a2ΘΫ4Θ§
Γύa2ΘΫ![]() Θ§
Θ§
Φ¥ΗΟ»ΐΫ«–Έ±Ώ≥ΛΒΡΤΫΖΫ «![]() ΘΜ
ΘΜ
ΔΎ≤Ι»ΪΆΦ–Έ»γΆΦ2Υυ ΨΘΜ
Δέ”…Χβ“β÷ΣΘ§PGΘΫPEΘ§GNΘΫNFΘ§
ΓύPN «ΓςGEFΒΡ÷–ΈΜœΏΘ§
ΓύPNΘΫ![]() EFΘ§
EFȧ
ΓΏNΈΣAB±Ώ…œΒΡ÷–ΒψΘ§
ΓύBNΘΫ![]() ABΘΫ1Θ§
ABΘΫ1Θ§
ΓΏ±Ώ≥ΛΈΣ2ΒΡ’ΐΖΫ–ΈΒΡΟφΜΐΘΫ4Θ§
ΓύΦτΤ¥≥…ΒΡΒ»±Ώ»ΐΫ«–ΈΒΡΟφΜΐΘΫ4Θ§
Γύ![]() a2ΘΫ4Θ§
a2ΘΫ4Θ§
Γύa2ΘΫ![]() Θ§
Θ§
Φ¥ΓςGEF±Ώ≥ΛΒΡΤΫΖΫ «![]() Θ§
Θ§
ΓύEFΘΫ![]() Θ§
Θ§
ΓύPNΘΫ![]() Θ§
Θ§
ΓΏPN2ΘΫBN2+BP2Θ§
Γύ![]() ΘΫ1+x2Θ§
ΘΫ1+x2Θ§
Γύx2ΘΫ![]() ©¹1ΘΜ
©¹1ΘΜ
Ι ¥πΑΗΈΣΘΚΘ®1Θ©![]() ΘΜΘ®2Θ©ΔΌ
ΘΜΘ®2Θ©ΔΌ![]() ΘΜΔέ
ΘΜΔέ![]() Θ°
Θ°