题目内容
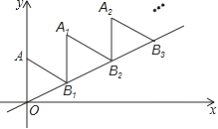
【题目】如图,已知![]() ,
,![]() 为线段
为线段![]() 上的一个动点,分别以
上的一个动点,分别以![]() ,
,![]() 为边在
为边在![]() 的同侧作菱形
的同侧作菱形![]() 和菱形
和菱形![]() ,点
,点![]() ,
,![]() ,
,![]() 在一条直线上,
在一条直线上,![]() ,
,![]() 、
、![]() 分别是对角线
分别是对角线![]() ,
,![]() 的中点,当点
的中点,当点![]() 在线段
在线段![]() 上移动时,线段
上移动时,线段![]() 的最小值为________.
的最小值为________.

【答案】![]()
【解析】
连接QC、PC,先证明∠PCQ=90°,设AC=![]() ,则BC=
,则BC=![]() ,PC=
,PC=![]() ,CQ=
,CQ=![]() (
(![]() ),构建二次函数,利用二次函数的性质即可解决问题.
),构建二次函数,利用二次函数的性质即可解决问题.
连接PC、CQ.
∵四边形ACED,四边形CBGF是菱形,∠D=120°,
∴∠ACE=120°,∠FCB=60°,
∵P,Q分别是对角线AE,BF的中点,
∴∠ECP=∠ACP=![]() ∠ACE=60°,∠FCQ=∠BCQ=
∠ACE=60°,∠FCQ=∠BCQ=![]() ∠BCF=30°,
∠BCF=30°,
∴∠PCQ=90°,
设AC=![]() ,则BC=
,则BC=![]() ,PC=
,PC=![]() AC=
AC=![]() ,CQ=BC
,CQ=BC![]() =
=![]() (
(![]() ),
),
∴ ,
,
∴当![]() 时,线段PQ有最小值,最小值为
时,线段PQ有最小值,最小值为![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】某蔬菜公司收购蔬菜进行销售的获利情况如下表所示:
销售方式 | 直接销售 | 粗加工后销售 | 精加工后销售 |
每吨获利/元 | 100 | 250 | 450 |
现在该公司收购了140吨蔬菜,已知该公司每天能精加工蔬菜6吨或粗加工蔬菜16吨(两种加工不能同时进行)。
(1)如果要求在18天内全部销售完这140吨蔬菜,请完成下列表格:
销售方式 | 全部直接销售 | 全部粗加工销售 | 尽量精加工,剩 余部分直接销售 |
获利/元 |
(2)如果先进行精加工,然后进行粗加工,要求在15天内刚好加工完140吨蔬菜,则应如何分配加工时间?
(3)如果要求蔬菜都要加工后销售,且公司获利不能少于42200元,问:至少将多少吨蔬菜进行精加工?