题目内容
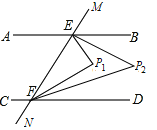
【题目】如图,已知直线AB∥CD,MN分别交AB,CD于点E,F,∠BEF与∠DFE的两条平分线相交于点P1,∠BEP1与∠DFP1的两条平分线相交于点P2,则∠P2的度数为_______.
【答案】![]()
【解析】
先证明∠P1=90°,再证明∠P2=![]() ,即可得到结论.
,即可得到结论.
过P1作P1G∥AB,可得P1G∥CD,如图(1)
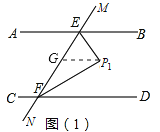
∴∠BE P1=∠EP1G,∠G P1F=∠P1FD,
∵EP1、FP1分别为∠BEF与∠EFD的平分线,
∴∠BE P1=∠FEP1,∠EFP1=∠DFP1,
∵AB∥CD,
∴∠BE P1+∠FEP1+∠EFP1+∠DFP1=180°,即2(∠BEP1+∠DFP1)=180°,
∴∠BEP1+∠DFP1=90°,
则∠EP1F=∠EP1G+∠GP1F=90°;
∵∠BEP1、∠DFP1的平分线相交于点P2,
∴∠BEP2=∠P1EP2,∠P1FP2=∠DFP2,
∵∠BEP1+∠FEP1+∠EFP1+∠DFP1=180°,即2(∠BEP1+∠P1FD)=180°,
∴∠BEP1+∠P1FD=90°,即∠P1EP2+∠P1FP2=45°,
∴∠P2=180°-(∠P1EF+∠EF P1)-(∠P1EP2+∠P1FP2)=45°.
故答案为:45°.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目