ЬтФПФкШн
ЁОЬтФПЁПВФСЯвЛЃКвЛИіДѓгк1ЕФе§ећЪ§ЃЌШєБЛ![]() Г§гр1ЃЌБЛ
Г§гр1ЃЌБЛ![]() Г§гр1ЃЌБЛ
Г§гр1ЃЌБЛ![]() Г§гр1ЁЁЃЌБЛ3Г§гр1ЃЌБЛ2Г§гр1ЃЌФЧУДГЦетИіе§ећЪ§ЮЊЁАУї
Г§гр1ЁЁЃЌБЛ3Г§гр1ЃЌБЛ2Г§гр1ЃЌФЧУДГЦетИіе§ећЪ§ЮЊЁАУї![]() РёЁБЪ§ЃЈ
РёЁБЪ§ЃЈ![]() ШЁзюДѓЃЉЃЌР§ШчЃК73ЃЈБЛ5Г§гр3ЃЉБЛ4Г§гр1ЃЌБЛ3Г§гр1ЃЌБЛ2Г§гр1ЃЌФЧУД73ЮЊЁАУїЫФРёЁБЪ§ЃЎ
ШЁзюДѓЃЉЃЌР§ШчЃК73ЃЈБЛ5Г§гр3ЃЉБЛ4Г§гр1ЃЌБЛ3Г§гр1ЃЌБЛ2Г§гр1ЃЌФЧУД73ЮЊЁАУїЫФРёЁБЪ§ЃЎ
ВФСЯЖўЃКЩш![]() ЃЌЁЁЃЌ3ЃЌ2ЕФзюаЁЙЋБЖЪ§ЮЊ
ЃЌЁЁЃЌ3ЃЌ2ЕФзюаЁЙЋБЖЪ§ЮЊ![]() ЃЌФЧУДЁАУї
ЃЌФЧУДЁАУї![]() РёЁБЪ§ПЩвдБэЪОЮЊ
РёЁБЪ§ПЩвдБэЪОЮЊ![]() ЃЈ
ЃЈ![]() ЮЊе§ећЪ§ЃЉЃЌР§ШчЃК6ЃЌ5ЃЌ4ЃЌ3ЃЌ2ЕФзюаЁЙЋБЖЪ§ЮЊ60ЃЌФЧУДЁАУїСљРёЁБЪ§ПЩвдБэЪОЮЊ
ЮЊе§ећЪ§ЃЉЃЌР§ШчЃК6ЃЌ5ЃЌ4ЃЌ3ЃЌ2ЕФзюаЁЙЋБЖЪ§ЮЊ60ЃЌФЧУДЁАУїСљРёЁБЪ§ПЩвдБэЪОЮЊ![]() ЃЈ
ЃЈ![]() ЮЊе§ећЪ§ЃЉ
ЮЊе§ећЪ§ЃЉ
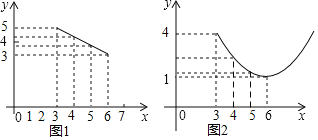
ЃЈ1ЃЉЧѓГізюаЁЕФШ§ЮЛЁАУїШ§РёЁБЪ§ЃЛ
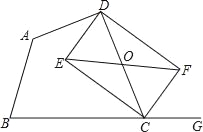
ЃЈ2ЃЉвЛИіЁАУїЫФРёЁБЪ§гыЁАУїЮхРёЁБЪ§ЕФКЭЮЊ170ЃЌЧѓГіетСНИіЪ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ17
ЃЈ2ЃЉ49ЃЛ121
ЁОНтЮіЁП
ЃЈ1ЃЉПЩжЊ3КЭ2ЕФзюаЁЙЋБЖЪ§ЪЧ6ЃЌЩшДЫЁАУїШ§РёЁБЪ§ЮЊ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЪЧе§ећЪ§ЃЌЕБЫќЪЧзюаЁЕФШ§ЮЛЪ§ЪБЃЌдђТњзу
ЪЧе§ећЪ§ЃЌЕБЫќЪЧзюаЁЕФШ§ЮЛЪ§ЪБЃЌдђТњзу![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ДгЖјЧѓГізюаЁЕФШ§ЮЛЁАУїШ§РёЁБЪ§.
ДгЖјЧѓГізюаЁЕФШ§ЮЛЁАУїШ§РёЁБЪ§.
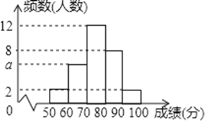
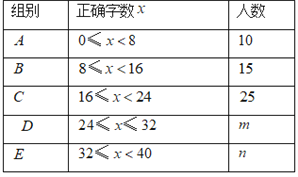
ЃЈ2ЃЉ4ЁЂ3ЁЂ2ЕФзюаЁЙЋБЖЪ§ЪЧ12ЃЌ5ЁЂ4ЁЂ3ЁЂ2ЕФзюаЁЙЋБЖЪ§ЪЧ60ЃЌЩшЁАУїЫФРёЁБЪ§ЪЧ![]() ЃЌЁАУїЮхРёЁБЪ§ЪЧ
ЃЌЁАУїЮхРёЁБЪ§ЪЧ![]() ЃЌИљОнвбжЊЬѕМўЁАУїЫФРёЁБЪ§гыЁАУїЮхРёЁБЪ§ЕФКЭЮЊ170ЃЌСаГіЕШЪНЃЌИљОн
ЃЌИљОнвбжЊЬѕМўЁАУїЫФРёЁБЪ§гыЁАУїЮхРёЁБЪ§ЕФКЭЮЊ170ЃЌСаГіЕШЪНЃЌИљОн![]() КЭ
КЭ![]() ЪЧе§ећЪ§ЬжТлМДПЩ.
ЪЧе§ећЪ§ЬжТлМДПЩ.
ЃЈ1ЃЉ3КЭ2ЕФзюаЁЙЋБЖЪ§ЪЧ6ЃЌЩшДЫЁАУїШ§РёЁБЪ§ЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]()
ЁрТњзуЩЯЪіЬѕМўЕФзюаЁе§ећЪ§ЪЧ17
ЃЈ2ЃЉ4ЁЂ3ЁЂ2ЕФзюаЁЙЋБЖЪ§ЪЧ12
5ЁЂ4ЁЂ3ЁЂ2ЕФзюаЁЙЋБЖЪ§ЪЧ60
ЩшЁАУїЫФРёЁБЪ§ЪЧ![]() ЃЌЁАУїЮхРёЁБЪ§ЪЧ
ЃЌЁАУїЮхРёЁБЪ§ЪЧ![]()
ЁпЁАУїЫФРёЁБЪ§гыЁАУїЮхРёЁБЪ§ЕФКЭЮЊ170
Ёр![]() +
+![]() =170
=170
гжЁп![]() КЭ
КЭ![]() ЪЧе§ећЪ§
ЪЧе§ећЪ§
Ёр![]() =4ЃЌ
=4ЃЌ![]() =2
=2
ЁретИіЁАУїЫФРёЁБЪ§ЪЧ49ЃЌЁАУїЮхРёЁБЪ§ЪЧ121

 аЁбЇЖсЙкABОэЯЕСаД№АИ
аЁбЇЖсЙкABОэЯЕСаД№АИ ABCПМЭѕШЋгХОэЯЕСаД№АИ
ABCПМЭѕШЋгХОэЯЕСаД№АИ