��Ŀ����
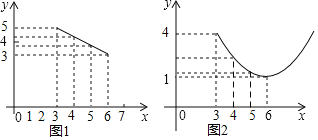
����Ŀ��ij���߲�ÿǧ���ۼ�y1��Ԫ���������·�x֮��Ĺ�ϵ��ͼ1��ʾ��ÿǧ�˳ɱ�y2��Ԫ���������·�x֮��Ĺ�ϵ��ͼ2��ʾ������ͼ1�еĵ���ͬһ���߶��ϣ�ͼ2�еĵ��ڶԳ���ƽ����y���ͬһ���������ϣ��������ߵ���͵������Ϊ(6��1)��
��1�����y1��x������ϵʽ��
��2�����y2��x������ϵʽ��
��3���������߲�ÿǧ������ΪwԪ���������ĸ��·ݳ��������߲ˣ�w��ȡ�����ֵ������������ֵ�������棽�ۼ۩��ɱ���
���𰸡���1��y1����![]() x+7����2��y2��
x+7����2��y2��![]() ��x��6��2+1����3��5�³��������߲ˣ�ÿǧ������������ֵ
��x��6��2+1����3��5�³��������߲ˣ�ÿǧ������������ֵ![]()
��������
��1�����ô���ϵ������y1��x֮������ĺ�������ʽ��
��2�����ö���ʽ��y2��x֮������ĺ�������ʽ��
��3���������棽�ۼ۩��ɱ����г���������ʽ�������䷽��������ֵ��
�⣺��1����y1��kx+b��
��ֱ�߾�����3��5������6��3����
![]() ��
��
��ã�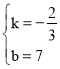 ��
��
��y1����![]() x+7��3��x��6����x��������
x+7��3��x��6����x��������
��2����y2��a��x��6��2+1��
�ѣ�3��4������ã�4��a��3��6��2+1��
���a��![]() ��
��
��y2��![]() ��x��6��2+1��
��x��6��2+1��
��3��������ã�w��y1��y2����![]() x+7��[
x+7��[![]() ��x��6��2+1]��
��x��6��2+1]��
����![]() ��x��5��2+
��x��5��2+![]() ��
��
��x��5ʱ��w���ֵ��![]() ��
��
��5�³��������߲ˣ�ÿǧ���������

����Ŀ��2018��ƽ�����»���2��9�յ�25���ں���ƽ�������У�Ϊ�˵�����ѧ���Զ��»������Ŀ���˽�̶ȣ�ij��ѧ��ѧ��������һ�γ������飬����������Ϊ�ĸ��ȼ���A���dz��˽�B���Ƚ��˽�C�������˽�D�����˽⣮���ݵ���ͳ�ƽ������������ͼ��ʾ�IJ�����������ͳ��ͼ����
�Զ��»��˽�̶ȵ�ͳ�Ʊ�
�Զ��»���˽�̶� | �ٷֱ� |
A�dz��˽� | 10% |
B�Ƚ��˽� | 15% |
C�����˽� | 35% |
D���˽� | n% |
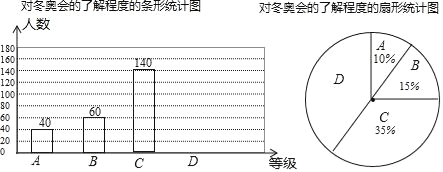
��1��n=�� ����
��2������ͳ��ͼ�У�D������������Ӧ��Բ�Ľ����� ����
��3���벹ȫ����ͳ��ͼ��
��4�����ݵ�������ѧУ����չ���»��֪ʶ������ij��Ҫ�����dz��˽����̶ȵ�С����С����ѡһ�˲μӣ��������������Ϸ��ȷ��˭��������������ǣ����ĸ���ȫ��ͬ��ƹ�����������1��2��3��4Ȼ��ŵ�һ�������Ĵ��У�һ�����ȴӴ�������һ������һ���ٴ�ʣ�µ����������������һ�������������������ϵ����ֺ�Ϊż������С��ȥ������С��ȥ�����û���״ͼ���б��ķ���˵�������Ϸ�Ƿ�ƽ��