题目内容
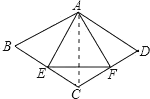
【题目】如图,菱形![]() 中,
中,![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() ,则
,则![]() 的周长为( )
的周长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
首先根据菱形的性质证明△ABE≌△ADF,然后连接AC可推出△ABC以及△ACD为等边三角形.根据等边三角形三线合一的性质又可推出△AEF是等边三角形.根据勾股定理可求出AE的长,继而求出周长.
解:∵四边形ABCD是菱形,
∴AB=AD=BC=CD=2cm,∠B=∠D,
∵E、F分别是BC、CD的中点,
∴BE=DF,
在△ABE和△ADF中,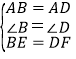 ,
,
∴△ABE≌△ADF(SAS),
∴AE=AF,∠BAE=∠DAF.
连接AC,
∵∠B=∠D=60°,
∴△ABC与△ACD是等边三角形,
∴AE⊥BC,AF⊥CD,
∴∠BAE=∠DAF=30°,
∴∠EAF=60°,BE=![]() AB=1cm,
AB=1cm,
∴△AEF是等边三角形,AE=![]() ,
,
∴周长是![]() .
.
故选:D.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
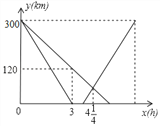
【题目】某工厂一个车间工人计划一周平均每天生产零件300个,实际每天生产量与计划每天生产量相比有误差.如表是这个车间工人在某一周每天的零件生产情况,超计划生产量为正、不足计划生产量为负.(单位:个)
时间 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
误差 | +10 | -15 | -6 | +12 | -10 | +18 | -11 |
(1)生产零件数量最少的一天比最多的一天少生产______个零件;
(2)若生产一个零件可得利润5元,则这个车间的工人在这一周为工厂一共带来了多少利润?