题目内容
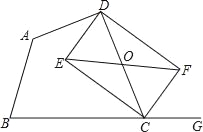
【题目】已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF平分∠GCD,EF∥BC交CD于点O.
(1)求证:OE=OF;
(2)若点O为CD的中点,求证:四边形DECF是矩形.
【答案】证明见解析
【解析】试题分析:(1)由角平分线的定义及平行线的性质可证得∠DCE=∠FEC,∠EFC=∠DCF,则可求得OE=OC=OF;
(2)利用(1)的结论,结合条件可证得四边形DECF为平行四边形,再利用角平分线的定义可求得∠ECF为直角,则可证得四边形DECF为矩形.
试题解析:解:(1)∵CE平分∠BCD、CF平分∠GCD,∴∠BCE=∠DCE,∠DCF=∠GCF.
∵EF∥BC,∴∠BCE=∠FEC,∠EFC=∠GCF,∴∠DCE=∠FEC,∠EFC=∠DCF,∴OE=OC,OF=OC,∴OE=OF;
(2)∵点O为CD的中点,∴OD=OC.又∵OE=OF,∴四边形DECF是平行四边形.
∵CE平分∠BCD、CF平分∠GCD,∴∠DCE=![]() ∠BCD,∠DCF=
∠BCD,∠DCF=![]() ∠DCG,∴∠DCE+∠DCF=
∠DCG,∴∠DCE+∠DCF=![]() (∠BCD+∠DCG)=90°,即∠ECF=90°,∴四边形DECF是矩形.
(∠BCD+∠DCG)=90°,即∠ECF=90°,∴四边形DECF是矩形.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目