题目内容
如图,梯形ABCD中,AD∥BC,AD=AB,BC=BD,∠A=100°,则∠C=( )
| A．80° | B．70° | C．75° | D．60° |
B
分析：先根据AD=AB求出∠ADB的度数，也就是∠DBC的度数，再根据BC=BD，即可求出∠C．
解答：解：∵AB=AD
∴∠ADB=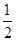
（180°-∠A）=40°
又∵AD∥BC
∴∠DBC=∠ADB=40°
又∵BC=BD
∴∠C=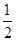（180°-∠DBC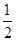）=（180°-40°）=70°．
故选B．
解答：解：∵AB=AD
∴∠ADB=
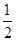（180°-∠A）=40°又∵AD∥BC
∴∠DBC=∠ADB=40°
又∵BC=BD
∴∠C=
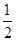（180°-∠DBC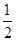）=（180°-40°）=70°．故选B．
练习册系列答案
科学实验活动册系列答案
相关题目
中，
将
顺时针旋转角
得
交
于点
，
分别交
于
两点．
与
有怎样的数量关系？并证明你的结论；
时，试判断四边形
的形状，并说明理由；
的长．
