题目内容
“十一黄金周”的某一天,小刚全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩,该小汽车离家的路程S(千米)与时间t (时)的关系可以用右图的折线表示。根据图象提供的有关信息,解答下列问题: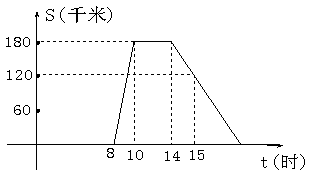
(1)小刚全家在旅游景点游玩了多少小时?
(2)求出整个旅程中S(千米)与时间t (时)的函数关系式,并求出相应自变量t的取值范围。
(3)小刚全家在什么时候离家120㎞?什么时候到家?
(1)4;(2)s=90t-720(8≤t≤10),s=180(10≤t≤14),s=-60t+1020(14≤t);(3)9时20分或15时,t=17.
解析试题分析:(1)根据图示,在旅游景点停留的时间可以知道游玩的时间.
(2)根据图象信息可以得出整个旅程中S(千米)与时间t (时)的函数关系式,讨论实际情况得到t的取值范围.
(3)从图中信息可知当t=8时,S=0,当t=10时,S=180,可算出去时距离120km时的时间,由图可知回来时当t=15时,S=120km.根据回来时的函数可得到家的时间.
试题解析:(1)由图示信息可知,在距离180千米的某著名旅游景点游玩,停留了4小时,所以游玩了14-10=4小时
(2)当8≤t≤10时
设s=kt+b过点(8,0),(10,180)
得s=90t-720.
当10≤t≤14时
s=180
当14≤t时
过点(14,180),(15,120)得
∴s=90t-720(8≤t≤10)
s=180(10≤t≤14)
s=-60t+1020(14≤t)
(3)当s=120km时,
90t-720=120得t=9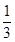
即9时20分
-60t+1020=120得t=15.
当s=0时
-60t+1020=0得t=17.
答:9时20分或15时离家120㎞,17时到家。
考点:一次函数的应用.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路.如果平均每天的修建费y(万元)与修建天数x(天)之间在30≤x≤120,具有一次函数的关系,如下表所示.
| x | 50 | 60 | 90 | 120 |
| y | 40 | 38 | 32 | 26 |
(2)后来在修建的过程中计划发生改变,政府决定多修2千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了15天,求原计划每天的修建费.
 的图象相交于点A(-2,a),并且与x轴相交于点B。
的图象相交于点A(-2,a),并且与x轴相交于点B。
 与
与 的图象相交于A点,函数
的图象相交于A点,函数 轴、
轴、 轴于点B,C,函数
轴于点B,C,函数
 的面积
的面积
 x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B'处.
x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B'处.

 与
与 成正比例,且当
成正比例,且当 时,
时, .
. 与
与 的函数关系式;
的函数关系式; 时的函数值.
时的函数值.