Question

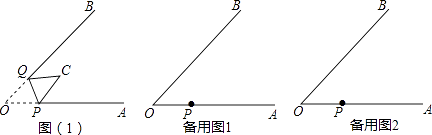
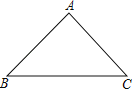
【题目】如图1，在△ABC中，∠B＝90°，∠C＝30°，点D从C点出发沿着CA方向以2个单位每秒的速度向终点A运动，同时点E从点A出发沿AB方向以1个单位每秒的速度向终点B运动。设点D，E的运动时间为t秒，DF⊥BC于F

（1）求证：AE＝DF；

（2）如图2，连接EF，

①是否存在t，使得四边形AEFD为菱形？若存在，求出t的值；若不存在，请说明理由

②连接DE，当△DEF是直角三角形时，求t的值

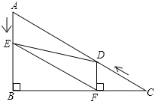
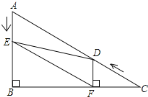
图1 图2 备用图 备用图

Answer 1

【答案】（1）见解析；（2）①存在；理由见解析，②当或t=4时，△DEF为直角三角形.

【解析】(1)在△DFC中，∠DFC=90°，∠C=30°，由已知条件求证；(2)①求得四边形AEFD为平行四边形，若使平行四边形AEFD为菱形则需要满足AE=AD即可求出t的值.②分三种情况：a.∠EDF=90°时，四边形EBFD为矩形．在直角三角形AED中求得AD=2AE即求得．b.∠DEF=90°时，由(2)知EF∥AD，则得∠ADE=∠DEF=90°，求得AD=AE·cos60°列式得．c.∠EFD=90°时，此种情况不存在．

（1）证明：∵在△DFC中，∠DFC=90°，∠C=30°，DC=2t

∴DF=t

又∵AE=t

∴AE=DF

（2）①存在；理由如下：

∵AB⊥BC，DF⊥BC，

∴AE∥DF，又AE=DF，

∴四边形AEFD为平行四边形

∵，

∴，

∴.

若使平行四边形AEFD为菱形，则需AE=AD，

即 ，

即当时，四边形AEFD为菱形。

②a. 若∠EDF=90°时，四边形EBFD为矩形，

在Rt△AED中，∠ADE=∠C=30°，

∴AD=2AE，即，；

b. 若∠DEF=90°，由平行四边形AEFD的性质知EF∥AD，

∴∠ADE=∠DEF=90°，

∵∠A=90°-∠C=60°，

∴AD=AE·cos60°，即，；

c. 若∠EFD=90°，此种情况不存在；

综上所述，当或时，△DEF为直角三角形.