题目内容
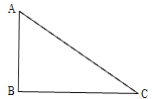
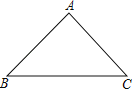
【题目】如图,已知△ABC
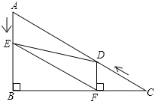
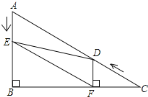
(1)用直尺和圆规作△ABC的边BC上的高AD,并在线段AD上找一点E,使E到AB的距离等于ED(不写作法,保留作图痕迹);
(2)若AB=AC=5,BC=6,求出ED的长。
【答案】(1)作图见解析;(2)1.5.
【解析】(1)直接作∠ABC的平分线的与高AD的交点E即可;
(2)利用等腰三角形的性质求出BD的长,利用勾股定理得到AD的长,利用角平分线的性质得到EF=ED,根据全等三角形的性质得到BF=BD,从而得到AF的长.在Rt△AFE中,利用勾股定理得出EF的长,从而可得答案.
(1)BC边上的高和∠ABC的角平分线交于点E;

(2)过E作EF⊥AB于F.设ED=x.
∵AB=AC,AD⊥BC,∴BD=![]() BC=3,∴AD=
BC=3,∴AD=![]() =
=![]() =4.
=4.
∵BE是∠ABD的平分线,∴EF=ED=x.
∵BE=BE,∴Rt△BEF≌Rt△BED,∴BF=BD=3,∴AF=5-3=2.在Rt△AEF中,∵AF2+EF2=AE2,∴22+x2= (4-x)2,解得:x=1.5.


练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目