题目内容
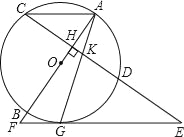
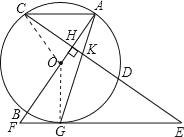
【题目】 如图,AB是⊙O的直径,弦CD⊥AB于点H,点G在弧BD上,连接AG,交CD于点K,过点G的直线交CD的延长线于点E,交AB的延长线于点F,且EG=EK.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为13,CH=12,![]()
![]() ,求FG的长.
,求FG的长.
【答案】(1)证明见解析;(2)FG=2![]() .
.
【解析】
(1)连接OG,首先证明∠EGK=∠EKG,再证明∠HAK+∠KGE=90°,进而得到∠OGA+∠KGE=90°即GO⊥EF,进而证明EF是⊙O的切线;
(2)连接CO,解直角三角形即可得到结论.
(1)证明:连接OG,
∵弦CD⊥AB于点H,
∴∠AHK=90°,
∴∠HKA+∠KAH=90°,
∵EG=EK,
∴∠EGK=∠EKG,
∵∠HKA=∠GKE,
∴∠HAK+∠KGE=90°,
∵AO=GO,
∴∠OAG=∠OGA,
∴∠OGA+∠KGE=90°,
∴GO⊥EF,
∴EF是⊙O的切线;
(2)解:连接CO,在Rt△OHC中,
∵CO=13,CH=12,
∴HO=5,
∴AH=8,
∵![]() =
=![]() ,
,
∴OF=15,
∴FG=![]() =
=![]() =2
=2![]() .
.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
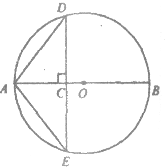
小夫子全能检测系列答案【题目】如图,⊙O的直径AB=4cm,点C为线段AB上一动点,过点C作AB的垂线交⊙O于点D,E,连结AD,AE.设AC的长为xcm,△ADE的面积为ycm2.
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量、分析,得到了y与x的几组对应值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm2 | 0 | 0.7 | 1.7 | 2.9 | 4.8 | 5.2 | 4.6 | 0 |
(2)如图,建立平面直角坐标系![]() ,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当△ADE的面积为4cm2时,AC的长度约为___________cm.