Question

【题目】如图，抛物线与轴交于，两点（点在点的左边）与轴交于点，连接，过点作直线的平行线交抛物线于另一点，交轴于点，则的值为__________．

Answer 1

【答案】

【解析】

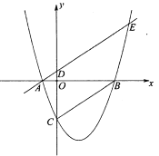
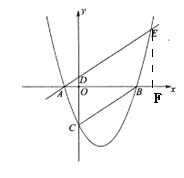
作EF⊥x轴与x轴交于点F，由抛物线y=a(x-4)(x+1)(a>0)得点A（-1,0）、B（4,0）、C（0，-4a），求出直线BC和直线AE的解析式，再求出直线AE和抛物线的交点可得点E的横坐标是5，则OF=5，由OD∥EF，根据平行线分线段成比例可得 .

解：作EF⊥x轴与x轴交于点F，

∵抛物线y=a(x-4)(x+1)(a>0)与轴交于A，B两点（点A在点的左边）与y轴交于点C，

∴A（-1,0）、B（4,0）、C（0，-4a），

设直线BC的解析式为 ，

，解得

∴直线BC的解析式为，

设直线AE的解析式为，

∵A（-1,0）∴-a+b=0,b=a,

∴直线AE的解析式为 ，

直线AE与抛物线y=a(x-4)(x+1)(a>0)的交点为

a(x-4)(x+1)=ax+a

解得

∴点E的横坐标为5，即OF=5，

∵OD∥EF

∴.

故答案为： .