��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A(��2, 0), C(0, 6)�����������y����![]() x2��ax��b��x�ύ����һ��B����D�������ߵĶ��㣮
x2��ax��b��x�ύ����һ��B����D�������ߵĶ��㣮
��1����a��b��ֵ��
��2����P��x���ϵ�һ�����㣬��P��ֱ��l//AC���������ڵ�Q�����ŵ�P���˶�������A��P��Q��CΪ������ı�����ƽ���ı��Σ���ֱ��д�����������ĵ�Q�����ꣻ
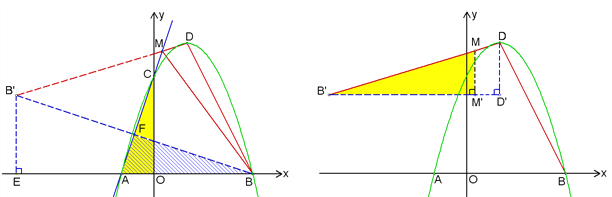
(3)��ֱ��AC���Ƿ����һ��M��ʹ��BDM���ܳ���С�������ڣ����ҳ���M�������M�����꣮�������ڣ���˵�����ɡ�


����ͼ
���𰸡���1��a=2��b=6��
��2��Q(4,6)��Q![]() ��
��![]() ��
��
��3������һ��M![]() ��ʹ��BDM���ܳ���С
��ʹ��BDM���ܳ���С
�������������������1���ѵ�A��C��������뵽����ʽ�У��ô���ϵ������������a��b��ֵ��
��2�����P��t��0��������ƽ���ı��ζ����λ�ò�ȷ����������Ҫ�������ۣ�����ƽ�Ƶ����ʣ��ú�t��ʽ�ӱ�ʾ����Q���������ѵ�Q��������뵽���κ����Ľ���ʽ�У����t������Եõ���Q������.
��3������B����ֱ��AC�ĶԳƵ�B��������BB������AC�ڵ�M�����M������Ҫ��ĵ�.����B����B��E��x�ᣬ�������������εõ�B�������꣬��B��DΪֱ�ǵ�б�߹���ֱ������������ɵõ�M������.
���������(1)���������![]() ����A��-2��0�������a=2.����a=2��b=6.
����A��-2��0�������a=2.����a=2��b=6.
��2����P��t,0��,�ɣ�1���ã�A��-2��0����C��0��6��.����ƽ�Ƶ����ʵã�
��![]() ��
�� ![]() ����Q��t+2��6��������
����Q��t+2��6��������![]() ����ã�
����ã� ![]() ��
�� ![]() ���ᣩ������Q��4��6��.
���ᣩ������Q��4��6��.
��![]() ��
�� ![]() ����Q��t-2��-6��������
����Q��t-2��-6��������![]() ����ã�
����ã� ![]() ��
�� ![]() ������Q��
������Q��![]() ��-6����
��-6����![]() ��-6��.
��-6��.
��![]() ��
�� ![]() ����Q��-t-2��6��������
����Q��-t-2��6��������![]() ����ã�
����ã� ![]() ���ᣩ.
���ᣩ.
����������Q(4,6)��Q��![]() ��-6����
��-6����![]() ��-6��.
��-6��.
��3�����B����ֱ��AC�ĶԳƵ�ΪB��������BB����AC��F��
����B��D��B��D��AC�Ľ������Ҫ��ĵ�M��
��B��E��x����E����ô��BB��E�ס�BAF�ס�CAO����AO=2��CO=6����AC=![]() B(6��0)��D(2��8).
B(6��0)��D(2��8).
��Rt��BAF�� ![]()
��Rt��BB��E�� ![]()
![]() .
.
��Ϊ��M��ֱ��y��3x��6�ϣ����M������Ϊ(x, 3x��6)��
��![]() ����
����![]()
 .
.
ͼ2 ͼ3