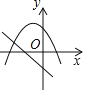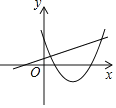题目内容
【题目】如图,⊙O的直径AB=4cm,点C为线段AB上一动点,过点C作AB的垂线交⊙O于点D,E,连结AD,AE.设AC的长为xcm,△ADE的面积为ycm2.
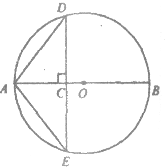
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量、分析,得到了y与x的几组对应值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm2 | 0 | 0.7 | 1.7 | 2.9 | 4.8 | 5.2 | 4.6 | 0 |
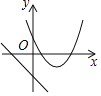
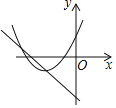
(2)如图,建立平面直角坐标系![]() ,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当△ADE的面积为4cm2时,AC的长度约为___________cm.
【答案】(1)见解析;(2)见解析;(3)2.0或3.7.
【解析】
(1) 设AC的长为2cm时,DE为直径,即可求出![]()
完成表格即可.
(2)根据(1)中的表格,描点,连线,即可画出该函数的图象;
(3)观察图象,即可得出△ADE的面积为4cm2,△ADE的面积为4cm2,即可求出AC的长.
本题答案不唯一,如:
(1)
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm2 | 0 | 0.7 | 1.7 | 2.9 | 4.0 | 4.8 | 5.2 | 4.6 | 0 |
(2)
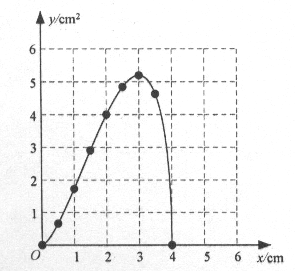
(3) 当△ADE的面积为4cm2时,AC的长度约为2.0或3.7.
故答案为:2.0或3.7.

 阅读快车系列答案
阅读快车系列答案【题目】电影公司随机收集了2000部电影的有关数据,经分类整理得到如表:
电影类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
电影部数 | 140 | 50 | 300 | 200 | 800 | 510 |
好评率 |
|
|
|
|
|
|
注:好评率是指一类电影中获得好评的部数与该类电影的部数的比值.
![]() 如果电影公司从收集的电影中随机选取1部,那么抽到的这部电影是获得好评的第四类电影的概率是______;
如果电影公司从收集的电影中随机选取1部,那么抽到的这部电影是获得好评的第四类电影的概率是______;
![]() 电影公司为了增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化
电影公司为了增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化![]() 假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加
假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加![]() ,哪类电影的好评率减少
,哪类电影的好评率减少![]() ,可使改变投资策略后总的好评率达到最大?
,可使改变投资策略后总的好评率达到最大?
答:______.