题目内容
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC,垂足为E.
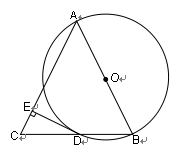
(1)求证:AB=AC;(2)求证DE为⊙O的切线.

(1)求证:AB=AC;(2)求证DE为⊙O的切线.
详见解析
试题分析:(1)如图,连接AD,由AB为直径可得AD⊥BD,又DC=BD,根据垂直平分线的性质可得AB=AC.
(2)要证DE为⊙O的切线,只要证明∠ODE=90°即可.可由点O、D分别是AB、BC的中点由中位线定理求得.
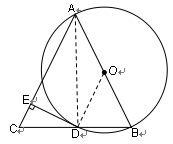
试题解析:
解:(1)证明:连结AD
∵AB是⊙O直径
∴∠ADB=90°
又∵CD=BD
∴AD是BC的垂直平分线
∴AB=AC
(2)连结DO
∵AB是⊙O直径
∴OA=OB
又∵CD=BD
∴DO是△ABC的中位线
∴DO∥AC
∵DE⊥AC
∴DE⊥DO
∴DE是⊙O的切线

练习册系列答案
相关题目
 所在圆的圆心为
所在圆的圆心为 ,半径
,半径 为3米.
为3米.
 的度数;
的度数;
 取3.14)
取3.14)
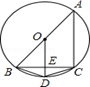
 线段DO的路线作匀速运动.设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )
线段DO的路线作匀速运动.设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )
 B.
B. C.
C. D.
D.

 cm
cm  cm
cm  cm
cm