题目内容
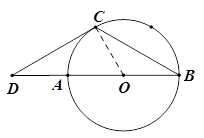
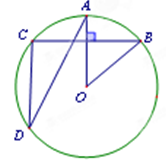
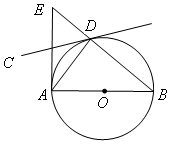
如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D使∠BDC=30°.
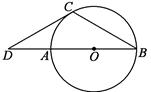
(1)求证:DC是⊙O的切线.
(2)若AB=2,求DC的长.

(1)求证:DC是⊙O的切线.
(2)若AB=2,求DC的长.
详见解析.
试题分析:(1)求证
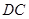 是⊙
是⊙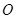 的切线,只需证明圆心到线段的距离等于半径即可.即求证
的切线,只需证明圆心到线段的距离等于半径即可.即求证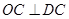 。因为弧
。因为弧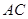 所对的圆心角
所对的圆心角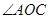 是其所对的圆周角
是其所对的圆周角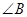 的2倍,所以
的2倍,所以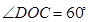 ,因为
,因为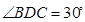 ,所以
,所以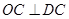 、
、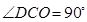 ,即
,即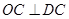 ,所以
,所以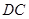 是⊙
是⊙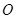 的切线.
的切线.(2)由(1)可知,所求
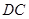 为
为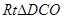 的一直角边,因此可用勾股定理求解。由
的一直角边,因此可用勾股定理求解。由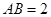 ,可得
,可得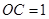 ,由
,由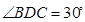 ,
,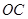
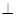
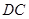 ,可得
,可得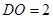 .所以
.所以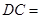
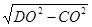 ,即
,即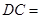
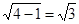 .
.
试题解析:
(1)证明:连接
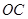
∵
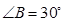
∴
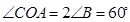
∵
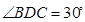
∴
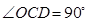
∵
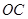 是⊙
是⊙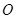 的半径
的半径∴
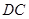 是⊙
是⊙ 的切线.
的切线.(2)解:∵
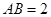
∴
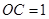
∵
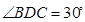 ,
,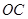
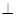
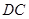
∴
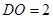
在
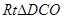 中,
中,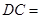
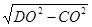
∴
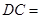

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
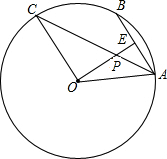
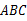 的三个顶点都在半径为5cm的⊙O上,如果底边
的三个顶点都在半径为5cm的⊙O上,如果底边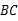 的长为8cm,则
的长为8cm,则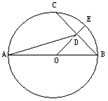
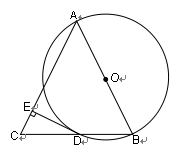
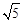 ,BD=2,求线段AE的长。
,BD=2,求线段AE的长。