��Ŀ����
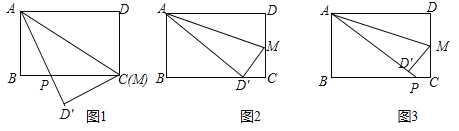
����Ŀ����ͼ�������ɸ���������״��ľ��ѳɵģ�ƽ���������ϡ����У�������������µ�����ĸ�����ǡ������������������ϵ�����ߵ��е㣬������������������ⳤΪ1��
��1����ֻ���������������һ��ʱ��������������¶�������������� ��
��2������Щ������¶�����������ͳ���![]() ʱ����ô������ĸ��������Ƕ��٣�
ʱ����ô������ĸ��������Ƕ��٣�
��3�����˹�����ȥ����Щ������¶�������������һֱ��������ᣬ��˵�����ɣ�������ᣬ��������ᳬ���ĸ���ֵ������ʾ������������������������������������¶�������֮�ͣ����������������Ӽ����֣����ɹ��ɣ���
���𰸡���1��7����2��4������3�����ᣬ���ɼ�����
��������
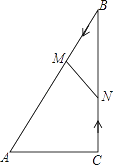
��1����ֻ��һ�㣨��ֻ��һ����ʱ��ÿ����������1����¶��5���棬������¶���Ϊ��1+1��4=5���������㣬��ڶ���ÿ������������![]() ����һ����ȣ�����4�����棬������¶���Ϊ��1+��1+
����һ����ȣ�����4�����棬������¶���Ϊ��1+��1+![]() ����4=7��
����4=7��
��2���������㣬��������ÿ������������![]() ����������ȣ�����4�����棬������¶���=1+��1+
����������ȣ�����4�����棬������¶���=1+��1+![]() +
+![]() ����4=8����Щ������¶�����������ͳ���8����ô������ĸ���������4����
����4=8����Щ������¶�����������ͳ���8����ô������ĸ���������4����
��3������n�㣬���ԣ�¶����������Ϊ��1+[1+![]() +
+![]() +����+
+����+![]() ]��4��1+2��4=9�������˹��ɶ���ȥ���������ᳬ��9��
]��4��1+2��4=9�������˹��ɶ���ȥ���������ᳬ��9��
�⣺��1����ֻ��һ�㣨��ֻ��һ����ʱ��ÿ����������1����¶��5���棬������¶���Ϊ��1+1��4=5��
�������㣬��ڶ���ÿ������������![]() ����һ����ȣ�����4�����棬������¶���Ϊ��1+��1+
����һ����ȣ�����4�����棬������¶���Ϊ��1+��1+![]() ����4=7��
����4=7��
��3���������㣬��������ÿ������������![]() ����������ȣ�����4�����棬������¶���=1+��1+
����������ȣ�����4�����棬������¶���=1+��1+![]() +
+![]() ����4=8��
����4=8��
����Щ������¶�����������ͳ���8����ô������ĸ���������4����
��3������n�㣬���ԣ�¶����������Ϊ��1+[1+![]() +
+![]() +����+
+����+![]() ]��4��1+2��4=9��
]��4��1+2��4=9��
�ఴ�˹��ɶ���ȥ���������ᳬ��9��

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�����Ŀ�����κ���y=ax2+bx+c��a��b��cΪ��������a��0���е�x��y�IJ��ֶ�Ӧֵ���±���
X | ��1 | 0 | 1 | 3 |
y | ��1 | 3 | 5 | 3 |
���н��ۣ�
��ac��0��
�Ƶ�x��1ʱ��y��ֵ��xֵ���������С��
��3�Ƿ���ax2+��b��1��x+c=0��һ������
�ȵ���1��x��3ʱ��ax2+��b��1��x+c��0��
������ȷ�ĸ���Ϊ����
A. 4�� B. 3�� C. 2�� D. 1��
����Ŀ��������y=��x2+bx+c�ϲ��ֵ�ĺ�����x��������y�Ķ�Ӧֵ���±���ʾ��
x | �� | ��2 | ��1 | 0 | 1 | 2 | �� |
y | �� | 0 | 4 | 6 | 6 | 4 | �� |
���ϱ���֪������˵���У�������ǣ�������
A. ��������x���һ����������Ϊ����2��0�� B. ��������y��Ľ�������Ϊ��0��6��
C. �����ߵĶԳ�����ֱ��x=0 D. �������ڶԳ�����ಿ����������