题目内容
【题目】已知长方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,由
上,由![]() 往
往![]() 运动,速度为
运动,速度为![]() ,运动时间为
,运动时间为![]() 秒,将
秒,将![]() 沿着
沿着![]() 翻折至
翻折至![]() ,点
,点![]() 对应点为
对应点为![]() ,
,![]() 所在直线与边
所在直线与边![]() 交与点
交与点![]() ,
,
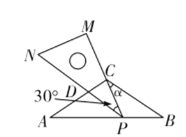
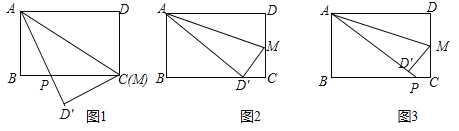
(1)如图![]() ,当
,当![]() 时,求证:
时,求证:![]() ;
;
(2)如图![]() ,当
,当![]() 为何值时,点
为何值时,点![]() 恰好落在边
恰好落在边![]() 上;
上;
(3)如图![]() ,当
,当![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据矩形的性质和折叠的性质可得![]() ,即可得
,即可得![]() ;
;
(2)由折叠的性质可得![]() =10cm,
=10cm,![]() ,根据勾股定理可求
,根据勾股定理可求![]() =8cm,即可得
=8cm,即可得![]() =2cm,根据勾股定理可求CM的长,即可求t的值;
=2cm,根据勾股定理可求CM的长,即可求t的值;
(3)连接MP,根据题意可得![]() ,根据“HL”可证
,根据“HL”可证![]() ≌
≌![]() ,可得
,可得![]() ,根据勾股定理可求CP的长.
,根据勾股定理可求CP的长.
证明:![]() 四边形ABCD是矩形
四边形ABCD是矩形![]()
![]() ,
,
根据折叠得,∠DAC=∠![]()
∴∠ACB=∠![]()
∴![]()
![]() 折叠
折叠
∴![]() =10cm,
=10cm,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
∴![]()
∴![]()
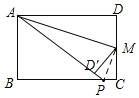
![]() 如图,连接MP,
如图,连接MP,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 折叠
折叠
∴![]() =10cm,
=10cm,![]() ,
,
∴![]() ,且
,且![]()
![]() ≌Rt△D′MP(HL)
≌Rt△D′MP(HL)
∴![]()
在![]() 中,
中,![]() ,
,
![]() ,
,
∴![]()

练习册系列答案
相关题目