题目内容
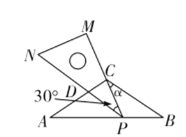
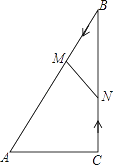
【题目】如图,在![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发, 在
出发, 在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,设运动时间为
匀速运动,设运动时间为![]() 秒
秒![]() ,连接
,连接![]() .
.
![]() 若
若![]() ,求
,求![]() 的值;
的值;
![]() 若
若![]() 与
与![]() 相似,求
相似,求![]() 的值;
的值;
![]() 当
当![]() 为何值时,四边形
为何值时,四边形![]() 的面积为
的面积为![]()
【答案】(1)![]() (2)当t=
(2)当t=![]() 或t=
或t=![]() 时,△MBN与△ABC相似.(3)当
时,△MBN与△ABC相似.(3)当![]() 或
或![]() 时,四边形
时,四边形![]() 的面积是
的面积是![]()
【解析】
(1)由已知条件得出AB=10,BC=![]() 由题意知:BM=2t,CN=
由题意知:BM=2t,CN=![]() ,BN=
,BN=![]() 由BM=BN得出方程2t=
由BM=BN得出方程2t=![]() 解方程即可;
解方程即可;
(2)分两种情况:①当△MBN∽△ABC时,由相似三角形的对应边成比例得出比例式,即可得出t的值; ②当△NBM∽△ABC时,由相似三角形的对应边成比例得出比例式,即可得出t的值;
(3)利用四边形![]() 的面积等于
的面积等于![]() 的面积减去
的面积减去![]() 的面积列方程求解即可.
的面积列方程求解即可.
解:(1)∵在Rt△ABC中,∠ACB=90°,AC=5,∠BAC=60°,
∴∠B=30°, ∴AB=2AC=10,BC=![]()
由题意知:BM=2t,CN=![]()
∴BN=![]()
∵BM=BN,
∴2t=![]()
解得:![]()
(2)分两种情况:①当△MBN∽△ABC时,
则 ![]()
即 ![]()
解得:![]()
②当△NBM∽△ABC时,
则![]()
即![]()
解得:![]()
综上所述:当t=![]() 或t=
或t=![]() 时,△MBN与△ABC相似.
时,△MBN与△ABC相似.
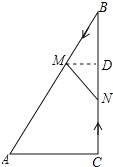
(3)由(1)知:∠ACB=90°,AC=5,AB=2AC=10,BC=![]()
![]()
过![]() 作
作![]() 于
于![]() ,
,
又![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 的面积为
的面积为![]() ,
,
![]()
![]()
解得:![]()
即当![]() 或
或![]() 时,四边形
时,四边形![]() 的面积为
的面积为![]() .
.

练习册系列答案
相关题目