Question

【题目】如图所示，点A在半径为20的圆O上，以OA为一条对角线作矩形OBAC，设直线BC交圆O于D、E两点，若OC=12，则线段CE、BD的长度差是_____．

Answer 1

【答案】

【解析】

设DE的中点为M，连接OM，则OM⊥DE，在Rt△AOB中利用勾股定理求出OB的长，利用三角形的面积公式求出OM的长，在Rt△OCM中，利用勾股定理求出CM的长，进而可得出BM的长，由CE-BD=（EM-CM）-（DM-BM）=BM-CM即可得出结论.

解：如图，设DE的中点为M，连接OM，则OM⊥DE．

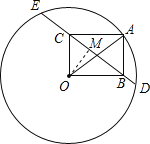
∵在Rt△AOB中，OA=20，AB=OC=12，

∴OB===16，

∴OM===，

在Rt△OCM中，

CM===，

∵BM=BC-CM=20-=，

∴CE-BD=（EM-CM）-（DM-BM）=BM-CM=-=．

故答案为：.