题目内容
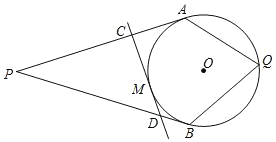
【题目】如图,PA、PB分别切⊙O于点A、B,M为劣弧AB上一点(不与A、B重合)过点M的切线分别与PA、PB相交于点C、D,Q为优弧AB上一点(不与A、B重合).
(1)若PA=10,求△PCD的周长;
(2)若∠P=40°,求∠AQB的度数.
【答案】(1)20;(2)70°.
【解析】
(1)根据切线长定理得到PA=PB,CA=CM,DM=DB,根据三角形的周长公式,用等线段代换计算即可.
(2)连接OA、OB,根据切线的性质可知,∠OAP=∠OBP=90,利用四边形内角和定理求得∠AOB=140,根据同弧所对的圆周角等于圆心角的一半,求得∠AQB=70.
(1)∵PA、PB分别切⊙O于点A、B,
∴PA=PB=10,
∵CD切⊙O于M,
∴CA=CM,DB=DM,
∵△PCD的周长=PC+CD+PD=PC+CM+PD+DM=PA+PB,
∴△PCD的周长=20;
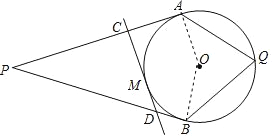
(2)连接OA,OB,
∵PA、PB分别切⊙O于点A、B,
∴∠PAO=∠PBO=90°,
∵∠P=40°,
∴∠AOB=140°,
∴∠AQB=![]() ∠AOB=70°.
∠AOB=70°.
故答案为:(1)20;(2)70°.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
【题目】某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了![]() 箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
第 | 第 | 第 | 第 | 第 | |
甲成绩 |
|
|
|
|
|
乙成绩 |
|
|
|
|
|
(1)a=_________
(2)![]()
(3)参照小宇的计算方法,计算乙成绩的方差;
(4)请你从平均数和方差的角度分析,谁将被选中.